
分析 (1)对x讨论,分x>0,x<0,由分式不等式的解法,即可得到解集;
(2)由题意可得$\frac{1}{{x}^{2}}$+x2+2m(x+$\frac{1}{x}$)≥0在x∈[1,2]上恒成立,即有(x+$\frac{1}{x}$)2-2+2m(x+$\frac{1}{x}$)≥0,令t=x+$\frac{1}{x}$,2≤t≤$\frac{5}{2}$,可得t2+2mt-2≥0,再由参数分离和函数的单调性,可得不等式的右边的最大值,可得m的范围;
(3)可令t=f(x),则g(t)=0,即有方程t=f(x)有6个实根,作出f(x)的图象,可得当x>0时,f(x)有最小值2,
则方程g(t)=0有两个大于2的不等实根,由二次方程实根分布解决方法,可得判别式大于0,g(2)大于0,对称轴大于2,解不等式即可得到所求范围.
解答 解:(1)f(x)≥2x,当x>0时,x+$\frac{1}{x}$≥2x,
即有x-$\frac{1}{x}$=$\frac{(x-1)(x+1)}{x}$≤0,解得0<x≤1;
当当x<0时,x-$\frac{1}{x}$≥2x,
即为x+$\frac{1}{x}$=$\frac{1+{x}^{2}}{x}$≤0,解得x<0.
故原不等式的解集为{x|x≤1且x≠0};
(2)$\frac{1}{{x}^{2}}$+x2+2mf(x)≥0在x∈[1,2]上恒成立,
即为$\frac{1}{{x}^{2}}$+x2+2m(x+$\frac{1}{x}$)≥0在x∈[1,2]上恒成立,
即有(x+$\frac{1}{x}$)2-2+2m(x+$\frac{1}{x}$)≥0,
令t=x+$\frac{1}{x}$,2≤t≤$\frac{5}{2}$,可得t2+2mt-2≥0,
即有m≥$\frac{1}{t}$-$\frac{t}{2}$,
令h(t)=$\frac{1}{t}$-$\frac{t}{2}$,h′(t)=-$\frac{1}{{t}^{2}}$-$\frac{1}{2}$<0,
则h(t)为单调递减函数,
则h(t)=$\frac{1}{t}$-$\frac{t}{2}$≤h(2)=$\frac{1}{2}$-1=-$\frac{1}{2}$,
即有m≥-$\frac{1}{2}$;
(3)函数g(x)=x2+(-3+c)x+c2,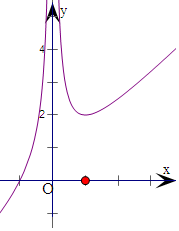
若方程g(f(x))=0有6个实根,
可令t=f(x),则g(t)=0,
即有方程t=f(x)有6个实根,
作出f(x)的图象,如右:
当x>0时,f(x)有最小值2,
则t>2,
方程g(t)=0有两个大于2的不等实根,
则$\left\{\begin{array}{l}{△=(c-3)^{2}-4{c}^{2}>0}\\{g(2)={c}^{2}+2c-2>0}\\{\frac{3-c}{2}>2}\end{array}\right.$即$\left\{\begin{array}{l}{-3<c<1}\\{c>\sqrt{3}-1或c<-\sqrt{3}-1}\\{c<-1}\end{array}\right.$,
可得-3<c<-$\sqrt{3}$-1.
点评 本题考查不等式的解法和恒成立问题的解法,以及方程根的分布情况,注意运用分类讨论和分离参数、以及数形结合的思想方法,考查化简运算能力,属于难题.


 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2016) | B. | (-2018,-2016) | C. | (-2016,-2) | D. | (-2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD是正方形,ED⊥平面ABCD,DE∥AF,AF=AD.
如图,四边形ABCD是正方形,ED⊥平面ABCD,DE∥AF,AF=AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{{{4^{\;}}}}+\frac{y^2}{3}=1$ | B. | $\frac{x^2}{{{4^{\;}}}}+\frac{y^2}{3}=1$(x<0) | ||
| C. | $\frac{y^2}{{{4^{\;}}}}+\frac{x^2}{3}=1$ | D. | $\frac{x^2}{{{4^{\;}}}}+\frac{y^2}{3}=1$(x>0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com