
【题目】在平面直角坐标系中,O为坐标原点,A、B、C三点满足 ![]() =
= ![]() +
+ ![]()
![]() .
.
(1)求证:A、B、C三点共线;
(2)求 ![]() 的值;
的值;
(3)已知A(1,cosx)、B(1+cosx,cosx),x∈[0, ![]() ],f(x)=
],f(x)= ![]()
![]() ﹣(2m+
﹣(2m+ ![]() )|
)| ![]() |的最小值为﹣
|的最小值为﹣ ![]() ,求实数m的值.
,求实数m的值.
【答案】
(1)证明:由已知 ![]() ,即
,即 ![]() ,
,
∴ ![]() ∥
∥ ![]() .又∵
.又∵ ![]() 、
、 ![]() 有公共点A,∴A,B,C三点共线.
有公共点A,∴A,B,C三点共线.
(2)解:∵ ![]() ,∴
,∴ ![]()
![]() =
= ![]()
![]() ∴
∴ ![]() ,∴
,∴ 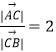 .
.
(3)解:∵C为 ![]() 的定比分点,λ=2,∴
的定比分点,λ=2,∴ ![]() ,
, ![]()
∴ ![]()
![]()
∵ ![]() ,∴cosx∈[0,1]
,∴cosx∈[0,1]
当m<0时,当cosx=0时,f(x)取最小值1与已知相矛盾;
当0≤m≤1时,当cosx=m时,f(x)取最小值1﹣m2,得 ![]() (舍)
(舍)
当m>1时,当cosx=1时,f(x)取得最小值2﹣2m,得 ![]()
综上所述, ![]() 为所求
为所求
【解析】(1)求证:A、B、C三点共线,可证由三点组成的两个向量共线,由题设条件不难得到;(2)由(1) ![]() 变形即可得到两向量模的比值;(3)求出
变形即可得到两向量模的比值;(3)求出 ![]() 的解析式,判断其最值取到的位置,令其最小值为-
的解析式,判断其最值取到的位置,令其最小值为- ![]() ,由参数即可,
,由参数即可,
【考点精析】认真审题,首先需要了解三角函数的最值(函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】一农民有基本农田2亩,根据往年经验,若种水稻,则每季每亩产量为400公斤;若种花生,则每季每亩产量为100公斤.但水稻成本较高,每季每亩240元,而花生只需80元,且花生每公斤5元,稻米每公斤卖3元.现该农民手头有400元,两种作物各种多少,才能获得最大收益?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是各项均为正数的数列,{bn}是等差数列,且a1=b1=1,a5﹣3b2=7.2a ![]() +(2﹣an+1)an﹣an+1=0(n∈N*)
+(2﹣an+1)an﹣an+1=0(n∈N*)
(1)求{an}和{bn}的通项公式;
(2)设cn=anbn , n∈N* , 求数列{cn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数字![]() 组成没有重复数字的四位数.
组成没有重复数字的四位数.
(Ⅰ)可组成多少个不同的四位数?
(Ⅱ)可组成多少个不同的四位偶数?
(Ⅲ)将(Ⅰ)中的四位数按从小到大的顺序排成一数列,问第![]() 项是什么?
项是什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位![]() 名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组
名员工参加“我爱阅读”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
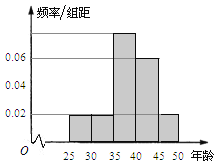
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(I)现要从年龄低于40岁的员工中用分层抽样的方法抽取12人,则年龄在第![]() 组的员工人数分别是多少?
组的员工人数分别是多少?
(II)为了交流读书心得,现从上述![]() 人中再随机抽取
人中再随机抽取![]() 人发言,设
人发言,设![]() 人中年龄在
人中年龄在![]() 的人数为
的人数为![]() ,求
,求![]() 的数学期望;
的数学期望;
(III)为了估计该单位员工的阅读倾向,现对从该单位所有员工中按性别比例抽取的40人做“是否喜欢阅读国学类书籍”进行调查,调查结果如下表所示:(单位:人)
喜欢阅读国学类 | 不喜欢阅读国学类 | 合计 | |
男 | 14 | 4 | 18 |
女 | 8 | 14 | 22 |
合计 | 22 | 18 | 40 |
根据表中数据,我们能否有![]() 的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系?
的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系?
附:![]() ,其中
,其中![]()
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面α∥平面β,P是α,β外一点,过点P的直线m与α,β分别交于点A,C,过点P的直线n与α,β分别交于点B,D,且PA=6,AC=9,PD=8,则BD的长为( )
A.![]()
B.![]()
C.![]() 或24
或24
D.![]() 或12
或12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用分期付款的方式购买某家用电器一件,价格为1 150元,购买当天先付150元,以后每月这一天还款一次,每次还款数额相同,20个月还清,月利率为1%,按复利计算.若交付150元后的第一个月开始算分期付款的第一个月,全部欠款付清后,请问买这件家电实际付款多少元?每月还款多少元?(最后结果保留4个有效数字)
参考数据:(1+1%)19=1.208,(1+1%)20=1.220,(1+1%)21=1.232.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足a3=2,前3项和为S3=![]() .
.
(1)求{an}的通项公式;
(2)设等比数列{bn}满足b1=a1,b4=a15,求{bn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com