解:(1)∵x≥1,∴4
x≥4,∴集合B={y|y≥4};
∵全集U=R,A={x|3≤x≤9},∴C
UA={x|x<3或x>9};
∴(C
UA)∩B={x|x<3或x>9}∩{y|y≥4}={x|x>9}.
(2)解:∵3≤x≤9,∴

,∴
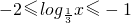
,∴C={y|-2≤y≤-1}.
∵C=D={x|x
2+ax+b≤0},
∴-2,-1是方程x
2+ax+b=0的两个根,
∴-2+(-1)=-a,(-2)×(-1)=b,
∴a=3,b=2,
∴a-b=1.
分析:(1)先利用补集的意义求出C
UA,利用指数函数的单调性化简集合B,进而利用交集的意义即可求出答案;
(2)先由对数函数的单调性化简出集合C,再根据一元二次不等式的解集与相应的一元二次方程的根的关系即可求出a、b.
点评:熟练掌握集合的运算法则、指数函数及对数函数的单调性和一元二次不等式的解法是解题的关键.

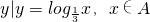 },D={x|x2+ax+b≤0}.
},D={x|x2+ax+b≤0}. ,∴
,∴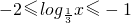 ,∴C={y|-2≤y≤-1}.
,∴C={y|-2≤y≤-1}.
