
在一次抢险救灾中,某救援队的50名队员被分别分派到四个不同的区域参加救援工作,其分布的情况如下表,从这50名队员中随机抽出2人去完成一项特殊任务.
| 区域 | A | B | C | D |
| 人数 | 20 | 10 | 5 | 15 |
(1) ;(2)分布列详见解析,数学期望
;(2)分布列详见解析,数学期望
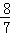
解析试题分析:(1)从50名队员中随机抽出2人去完成一项特殊任务,且2人来自同一区域分为四种情况,分别求概率,再根据互斥事件的概率求和公式计算;(2)基本事件总数为 ,
, 的取值有三种情况:当
的取值有三种情况:当 时,那么所选的两人都来自于D,有
时,那么所选的两人都来自于D,有 种;当
种;当 时,一人来自于A,一人来自于D,有
时,一人来自于A,一人来自于D,有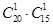 种;当
种;当 时,所选两人全部来自于A,有
时,所选两人全部来自于A,有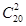 ,分别计算其概率,并写出随机变量
,分别计算其概率,并写出随机变量 分布列,进而再求数学期望.
分布列,进而再求数学期望.
试题解析:(1)记“这2人来自同一区域”为事件E,那么P(E)= =
= ,
,
所以这2人来自同一区域的概率是 .
.
(2)随机变量ξ可能取的值为0,1,2,且
P(X=0)=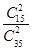 =
= ,P(X =1)=
,P(X =1)= =
= ,P(X =2)=
,P(X =2)=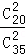 =
=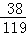
所以ξ的分布列是:
ξ的数学期望为Eξ=0×X 0 1 2 P 

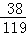
 +1×
+1× +2×
+2×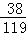 =
=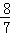
考点:1、古典概型和互斥事件的概率;2、离散型随机变量的分布列和期望.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
某商家推出一款简单电子游戏,弹射一次可以将三个相同的小球随机弹到一个正六边形的顶点与中心共七个点中的三个位置上(如图),用S表示这三个球为顶点的三角形的面积.规定:当三球共线时,S=0;当S最大时,中一等奖,当S最小时,中二等奖,其余情况不中奖,一次游戏只能弹射一次.
(1)求甲一次游戏中能中奖的概率;
(2)设这个正六边形的面积是6,求一次游戏中随机变量S的分布列及期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个盒子中装有形状大小相同的5张卡片,上面分别标有数字1,2,3,4,5,甲乙两人分别从盒子中随机不放回的各抽取一张.
(Ⅰ)写出所有可能的结果,并求出甲乙所抽卡片上的数字之和为偶数的概率;
(Ⅱ)以盒子中剩下的三张卡片上的数字作为边长来构造三角形,求出能构成三角形的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
据民生所望,相关部门对所属单位进行整治性核查,标准如下表:
规定初查累计权重分数为10分或9分的不需要复查并给予奖励,10分的奖励18万元;9分的奖励8万元;初查累计权重分数为7分及其以下的停下运营并罚款1万元;初查累计权重分数为8分的要对不合格指标进行复查,最终累计权重得分等于初查合格部分与复查部分得分的和,最终累计权重分数为10分方可继续运营,否则停业运营并罚款1万元.
(1)求一家单位既没获奖励又没被罚款的概率;
(2)求一家单位在这次整治性核查中所获金额X(万元)的分布列和数学期望(奖励为正数,罚款为负数).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一中食堂有一个面食窗口,假设学生买饭所需的时间互相独立,且都是整数分钟,对以往学生买饭所需的时间统计结果如下:
| 买饭时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市职教中心组织厨师技能大赛,大赛依次设基本功(初赛)、面点制作(复赛)、热菜烹制(决赛)三个轮次的比赛,已知某选手通过初赛、复赛、决赛的概率分别是 ,
,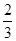 ,
, 且各轮次通过与否相互独立.
且各轮次通过与否相互独立.
(I)设该选手参赛的轮次为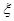 ,求
,求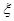 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)对于(I)中的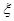 ,设“函数
,设“函数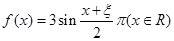 是偶函数”为事件D,求事件D发生的概率.
是偶函数”为事件D,求事件D发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n。如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验。
假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为,且各件产品是否为优质品相互独立
(1)求这批产品通过检验的概率;
(2)已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商场为吸引顾客消费推出一项促销活动,促销规则如下:到该商场购物消费满100元就可转动如图所示的转盘一次,进行抽奖(转盘为十二等分的圆盘),满200元转两次,以此类推;在转动过程中,假定指针停在转盘的任一位置都是等可能的;若转盘的指针落在A区域,则顾客中一等奖,获得10元奖金;若转盘落在B区域或C区域,则顾客中二等奖,获得5元奖金;若转盘指针落在其他区域,则不中奖(若指针停到两区间的实线处,则重新转动).若顾客在一次消费中多次中奖,则对其奖励进行累加.已知顾客甲到该商场购物消费了268元,并按照规则参与了促销活动.
(1)求顾客甲中一等奖的概率;
(2)记X为顾客甲所得的奖金数,求X的分布列及其数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com