
【题目】已知函数f(x)= ![]() 在x=1处取得极值.
在x=1处取得极值.
(1)求函数y=f(x)的单调区间;
(2)当x∈[1,+∞)时,f(x)≥ ![]() 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)当n∈N* , n≥2时,求证:nf(n)<2+ ![]() +
+ ![]() +…+
+…+ ![]() .
.
【答案】
(1)解:由题意得 ![]() ,
,
所以f'(1)=1﹣a=0即a=1,∴ ![]() ,
,
令f'(x)>0,可得0<x<1,令f'(x)<0,可得x>1,
所以f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.
(2)解:由题意要使x∈[1,+∞)时, ![]() 恒成立,
恒成立,
即 ![]() ,
,
记 ![]() ,则m≤[h(x)]min,
,则m≤[h(x)]min,
![]() ,又令g(x)=x﹣lnx,
,又令g(x)=x﹣lnx,
则 ![]() ,又x≥1,所以
,又x≥1,所以 ![]() ,
,
所以g(x)在[1,+∞)上单调递增,
即g(x)≥g(1)=1>0,
∴ ![]() ,
,
即h(x)在[1,+∞)上单调递增,
所以[h(x)]min=h(1)=2,∴m≤2.
(3)解:∵函数f(x)在区间(1,+∞)上单调递减,
而 ![]() (n∈N*,n≥2),
(n∈N*,n≥2),
∴ ![]() ,
,
∴ ![]() ,
,
即 ![]() ,
,
∴ ![]() ,
,
即 ![]() ,而nf(n)=1+lnn,
,而nf(n)=1+lnn,
∴ ![]() 结论成立.
结论成立.
【解析】(1)求出函数的导数,求出a的值,解关于导函数的不等式,求出函数的单调区间即可;(2)问题转化为 ![]() ,令
,令 ![]() ,根据函数的单调性求出h(x)的最小值,从而求出m的范围即可;(3)求出ln(n+1)﹣lnn<
,根据函数的单调性求出h(x)的最小值,从而求出m的范围即可;(3)求出ln(n+1)﹣lnn< ![]() ,结合nf(n)=1+lnn,证出结论即可.
,结合nf(n)=1+lnn,证出结论即可.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减),还要掌握函数的最大(小)值与导数(求函数
在这个区间单调递减),还要掌握函数的最大(小)值与导数(求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值)的相关知识才是答题的关键.
比较,其中最大的是一个最大值,最小的是最小值)的相关知识才是答题的关键.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】某食品的保鲜时间t(单位:小时)与储藏温度x(单位:℃)满足函数关系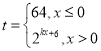 且该食品在4℃的保鲜时间是16小时.
且该食品在4℃的保鲜时间是16小时.
已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示.给出以下四个结论:

①该食品在6℃的保鲜时间是8小时;
②当x∈[﹣6,6]时,该食品的保鲜时间t随着x增大而逐渐减少;
③到了此日13时,甲所购买的食品还在保鲜时间内;
④到了此日14时,甲所购买的食品已然过了保鲜时间.
其中,所有正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为平行四边形,且AC=BD,平面PA⊥平面ABCD,E为PD的中点. 
(1)证明:PB∥平面AEC;
(2)在△PAD中,AP=2,AD=2 ![]() ,PD=4,三棱锥E﹣ACD的体积是
,PD=4,三棱锥E﹣ACD的体积是 ![]() ,求二面角D﹣AE﹣C的大小.
,求二面角D﹣AE﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形.
的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形.
(1)求椭圆的方程;
(2)过点M分别作直线MA,MB交椭圆于A,B两点,设两直线的斜率分别为k1 , k2 , 且k1+k2=8,证明:直线AB过定点( ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若椭圆![]() 和椭圆
和椭圆![]() 的焦点相同且
的焦点相同且![]() .给出如下四个结论:
.给出如下四个结论:
①椭圆![]() 与椭圆
与椭圆![]() 一定没有公共点 ②
一定没有公共点 ②![]()
③![]() ④
④![]()
其中所有正确结论的序号是( )
A. ①②③ B. ①③④ C. ①②④ D. ②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线f(x)=ke﹣2x在点x=0处的切线与直线x﹣y﹣1=0垂直,若x1 , x2是函数g(x)=f(x)﹣|1nx|的两个零点,则( )
A.1<x1x2< ![]()
B.![]() <x1x2<1
<x1x2<1![]()
C.2<x1x2<2 ![]()
D.![]() <x1x2<2
<x1x2<2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com