
(本小题满分13分)
在锐角 中,已知内角
中,已知内角 .
. .
. 所对的边分别为
所对的边分别为 .
. .
. ,向量
,向量
 ,
,
 ,且向量
,且向量 共线.
共线.
(1)求角 的大小;
的大小;
(2)如果 ,求
,求 的面积
的面积 的最大值.
的最大值.
解:(1)由向量 共线有:
共线有: 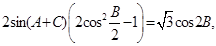
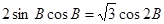 …………………………………………2分
…………………………………………2分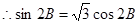 即
即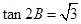 ,……………………… 4分
,……………………… 4分
又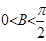 ,所以
,所以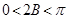 ,则
,则 =
=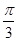 ,即
,即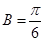 …………………6分
…………………6分
(2)由余弦定理得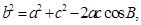 即
即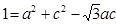 ……7分
……7分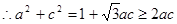 ,当且仅当
,当且仅当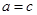 时等号成立……………9分
时等号成立……………9分
所以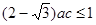 , 得
, 得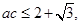
所以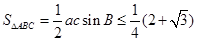 .……………………………… 12分
.……………………………… 12分
所以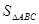 的最大值为
的最大值为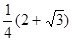 ……………………………… 13分
……………………………… 13分
解析试题分析:(1)根据共线向量的坐标满足的关系得到一个关系式,利用二倍角的正弦函数公式及同角三角函数间的基本关系化简,即可求出tan2B的值,然后由锐角B的范围求出2B的范围,利用特殊角的三角函数值即可求出B的度数;
(2)由b,cosB的值,利用余弦定理及基本不等式即可求出ac的最大值,根据三角形的面积公式进而得到三角形ABC面积的最大值。
解:(1)由向量 共线有:
共线有: 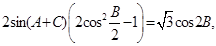
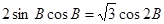 …………………………………………2分
…………………………………………2分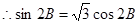 即
即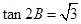 ,……………………… 4分
,……………………… 4分
又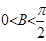 ,所以
,所以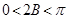 ,则
,则 =
=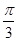 ,即
,即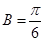 …………………6分
…………………6分
(2)由余弦定理得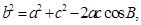 即
即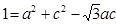 ……7分
……7分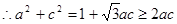 ,当且仅当
,当且仅当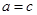 时等号成立……………9分
时等号成立……………9分
所以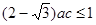 , 得
, 得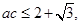
所以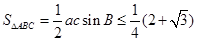 .……………………………… 12分
.……………………………… 12分
所以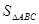 的最大值为
的最大值为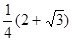 ……………………………… 13分
……………………………… 13分
考点:本试题主要考查了掌握向量关系时满足的条件,灵活运用二倍角的正弦函数公式及同角三角函数间的基本关系化简求值,灵活运用余弦定理及三角形的面积公式化简求值,是一道中档题.。
点评:解决该试题的难点是运用均值不等式得到ac的最大值。


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
已知向量m=(2sinx,cosx),n=(cosx,2cosx),定义函数f(x)=m·n-1.
(1)求函数f(x)的最小正周期;
(2)确定函数f(x)的单调区间、对称轴与对称中心.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com