
已知向量m=(2sinx,cosx),n=(cosx,2cosx),定义函数f(x)=m·n-1.
(1)求函数f(x)的最小正周期;
(2)确定函数f(x)的单调区间、对称轴与对称中心.
(1) ;(2)f(x)的单调递增区间是(kπ-
;(2)f(x)的单调递增区间是(kπ- ,kπ+),k∈Z;f(x)的单调递减区间是(kπ+,kπ+
,kπ+),k∈Z;f(x)的单调递减区间是(kπ+,kπ+ ),k∈Z;函数f(x)的对称轴为
),k∈Z;函数f(x)的对称轴为 ,k∈Z;函数f(x)的对称中心为
,k∈Z;函数f(x)的对称中心为 ,k∈Z .
,k∈Z .
解析试题分析:(1)根据向量数量积的坐标运算得到函数 的解析式,化为标准式,然后利用周期公式
的解析式,化为标准式,然后利用周期公式 来求;(2) 根据正弦曲线的单调区间:
来求;(2) 根据正弦曲线的单调区间: 单调递增,
单调递增, 单调递减求目标函数的单调区间,对称轴是根据
单调递减求目标函数的单调区间,对称轴是根据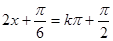 来求;对称中心是根据
来求;对称中心是根据 来求.
来求.
试题解析:(1)因为m·n=2sinxcosx+2cos2x 2分
=sin2x+cos2x+1, 4分
所以f(x)=2sin(2x+),
故T==π. 6分
(2)f(x)的单调递增区间是(kπ- ,kπ+),k∈Z, 8分
,kπ+),k∈Z, 8分
f(x)的单调递减区间是(kπ+,kπ+ ),k∈Z. 10分
),k∈Z. 10分
函数f(x)的对称轴为 ,k∈Z, 12分
,k∈Z, 12分
函数f(x)的对称中心为 ,k∈Z 14分
,k∈Z 14分
考点:平面向量、三角函数的图像与性质.


科目:高中数学 来源: 题型:解答题
如图所示,角A为钝角,且sin A= ,点P,Q分别是在角A的两边上不同于点A的动点.
,点P,Q分别是在角A的两边上不同于点A的动点.
(1)若AP=5,PQ=3 ,求AQ的长;
,求AQ的长;
(2)若∠APQ=α,∠AQP=β,且cos α= ,求sin(2α+β)的值.
,求sin(2α+β)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com