
分析 (1)把f(x),g(x)代入y=f(x)-g(x),求出导函数,再由在x=1与x=$\frac{1}{2}$时的导数值相等求得a的值,并进一步求得切线的斜率;
(2)由题意可得,函数y=f(x)-g(x)在区间($\frac{1}{3}$,1)上的导函数小于0恒成立,分离参数a,再由导数求得函数h(x)=$\frac{1}{{x}^{2}}-\frac{2}{x}$在区间($\frac{1}{3}$,1)上的范围得答案.
解答 解:(1)由f(x)=lnx,g(x)=$\frac{1}{2}$ax2+2x,得y=lnx-$\frac{1}{2}$ax2-2x,
∴y′=$\frac{1}{x}-ax-2$,
则y′|x=1=-a-1,$y′{|}_{x=\frac{1}{2}}=-\frac{a}{2}$,
由题意,$-a-1=-\frac{a}{2}$,解得a=-2.
∴k=1;
(2)函数y=f(x)-g(x)=lnx-$\frac{1}{2}$ax2-2x在区间($\frac{1}{3}$,1)上单调递减,
则y′=$\frac{1}{x}-ax-2$在区间($\frac{1}{3}$,1)上小于0恒成立,
即$\frac{1}{x}-ax-2$<0,分离参数a,得a>$\frac{1}{{x}^{2}}-\frac{2}{x}$.
令h(x)=$\frac{1}{{x}^{2}}-\frac{2}{x}$,则h′(x)=$\frac{2(x-1)}{{x}^{3}}$,
当x∈($\frac{1}{3}$,1)时,h′(x)<0,
∴h(x)在($\frac{1}{3}$,1)上为减函数,
则h(x)<h($\frac{1}{3}$)=3.
∴a≥3.
点评 本题考查利用导数研究过曲线上某点处的切线方程,考查了利用导数研究函数的单调性,训练了分离参数法求字母的取值范围,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2$\sqrt{3}$-1) | B. | (-∞,-2$\sqrt{3}$+1) | C. | (-2$\sqrt{3}$+1,2$\sqrt{3}$-1) | D. | (-2$\sqrt{3}$+1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
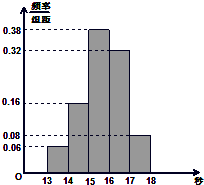 某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),第五组[17,18],图是按上述分组方法得到的频率分布直方图.
某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),第五组[17,18],图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com