
| A. | 大前提错误 | B. | 小前提错误 | C. | 结论正确 | D. | 推理形式错误 |
分析 在使用三段论推理证明中,如果命题是错误的,则可能是“大前提”错误,也可能是“小前提”错误,也可能是推理形式错误,我们分析的其大前提的形式:“若函数f(x)在区间(a,b)内无极值点,则f′(x)在区间(a,b)内无零点,不难得到结论.
解答 解:∵函数f(x)的导数为f′(x).若函数f(x)在区间(a,b)内无极值点,则f′(x)在区间(a,b)内无零点,是假命题,
∴大前提错误,
故选:A.
点评 本题考查的知识点是演绎推理的基本方法,演绎推理是一种必然性推理,演绎推理的前提与结论之间有蕴涵关系.因而,只要前提是真实的,推理的形式是正确的,那么结论必定是真实的,但错误的前提可能导致错误的结论.


科目:高中数学 来源: 题型:选择题
| A. | a>b=c | B. | b>a=c | C. | b>c>a | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
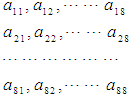 64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,每一列的数都成等比数列且每列数的公比都等于q,且a11=$\frac{1}{2}$,a24=1,a32=$\frac{1}{4}$.
64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,每一列的数都成等比数列且每列数的公比都等于q,且a11=$\frac{1}{2}$,a24=1,a32=$\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②①③ | B. | ③①② | C. | ①②③ | D. | ②③① |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com