C
分析:对于①把函数的解析式变形,再利用余弦函数的增区间是[2kπ-π,2kπ],k∈z,列出不等式,求得自变量x的取值范围.判断正误即可.
对于②,由于x=a 是函数的对称轴,且函数的周期等于π,可得 f(a+

)>f(a+

),判断②正误.
对于③,由于点
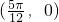
在函数图象上,结合图象可得函数图象关于点
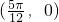
)对称,判断③的正误.
对于④代入

,函数取得最值,即可判断正误.
对于⑤利用函数的图象的平移,求出平移的函数的解析式,即可判断正误.
解答:①函数y=cos(

-3x)=cos(3x-

),根据余弦函数的增区间是[2kπ-π,2kπ],k∈z,
得:2kπ-π≤3x-

≤2kπ+

,解得

kπ-

≤x≤

kπ+

,k∈Z,故①正确.
对于②函数f(x)=5sin(2x+?),若f(a)=5,故x=a 是函数的对称轴,且函数的周期等于π,
故函数在[a-

,a+

]上是单调增函数.
∵f(a+

)=f(a-

),f(a+

)=f(a-

),a-

<a-

,
∴f( a-

)<f( a-

),即 f(a+

)>f(a+

);故②不正确.
对于③函数
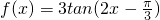
,由于点
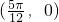
在图象上,结合图象可得函数图象关于点
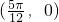
对称,
故③正确.
对于④当

代入函数

,函数取得最大值,所以

是函数图象的一条对称轴,故④正确.
对于⑤将函数y=sin
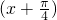
的图象向右平移

个单位,得到函数y=sinx的图象,故⑤不正确.
所以①③④.
故选C.
点评:本题主要考查三角函数的对称性和单调性,以及函数图象的变换,三角函数的内容比较琐碎,要记忆的比较多,平时要注意公式的记忆和基础知识的积累,掌握基本知识是解好这类题目的关键.

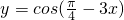 的递增区间是
的递增区间是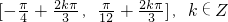 ;
; )<f(a+
)<f(a+ );
);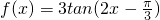 的图象关于点
的图象关于点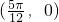 对称;
对称; 是函数
是函数 图象的一条对称轴;
图象的一条对称轴;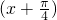 的图象向右平移
的图象向右平移 个单位得到.
个单位得到. )>f(a+
)>f(a+ ),判断②正误.
),判断②正误.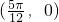 在函数图象上,结合图象可得函数图象关于点
在函数图象上,结合图象可得函数图象关于点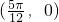 )对称,判断③的正误.
)对称,判断③的正误. ,函数取得最值,即可判断正误.
,函数取得最值,即可判断正误. -3x)=cos(3x-
-3x)=cos(3x- ),根据余弦函数的增区间是[2kπ-π,2kπ],k∈z,
),根据余弦函数的增区间是[2kπ-π,2kπ],k∈z, ≤2kπ+
≤2kπ+ ,解得
,解得  kπ-
kπ- ≤x≤
≤x≤ kπ+
kπ+ ,k∈Z,故①正确.
,k∈Z,故①正确. ,a+
,a+ ]上是单调增函数.
]上是单调增函数. )=f(a-
)=f(a- ),f(a+
),f(a+ )=f(a-
)=f(a- ),a-
),a- <a-
<a- ,
, )<f( a-
)<f( a- ),即 f(a+
),即 f(a+ )>f(a+
)>f(a+ );故②不正确.
);故②不正确.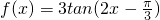 ,由于点
,由于点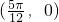 在图象上,结合图象可得函数图象关于点
在图象上,结合图象可得函数图象关于点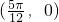 对称,
对称, 代入函数
代入函数 ,函数取得最大值,所以
,函数取得最大值,所以 是函数图象的一条对称轴,故④正确.
是函数图象的一条对称轴,故④正确.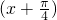 的图象向右平移
的图象向右平移 个单位,得到函数y=sinx的图象,故⑤不正确.
个单位,得到函数y=sinx的图象,故⑤不正确.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 的递增区间是
的递增区间是 ;
; )<f(a+
)<f(a+ );
); 的图象关于点
的图象关于点 对称;
对称; 是函数
是函数 图象的一条对称轴;
图象的一条对称轴; 的图象向右平移
的图象向右平移 个单位得到.
个单位得到. 的递增区间是
的递增区间是 ;
; )<f(a+
)<f(a+ );
); 的图象关于点
的图象关于点 对称;
对称; 是函数
是函数 图象的一条对称轴;
图象的一条对称轴; 的图象向右平移
的图象向右平移 个单位得到.
个单位得到. 的递增区间是
的递增区间是 ;
; ;
;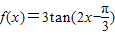 的图象关于点
的图象关于点 对称;
对称; 的图象向右平移
的图象向右平移 个单位,得到函数y=sin2x的图象;
个单位,得到函数y=sin2x的图象; 的图象和直线
的图象和直线 的交点个数是1个.
的交点个数是1个.