
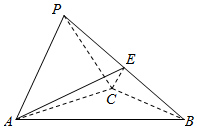
 如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,AP⊥PB,且AB=2$\sqrt{2}$,AC=BC=2,E为PB边的中点.
如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,AP⊥PB,且AB=2$\sqrt{2}$,AC=BC=2,E为PB边的中点.分析 (Ⅰ)在△ACB中,利用已知结合勾股定理可得AC⊥BC,再由面面垂直的性质可得BC⊥PA,由线面垂直的判定得PA⊥面PBC,则有AP⊥PC;
(Ⅱ)求解直角三角形可得三角形PCB的面积,结合E为PB边的中点得三角形PCE的面积,再求解直角三角形求得PA,代入棱锥体积公式求得三棱锥A-PEC的体积.
解答 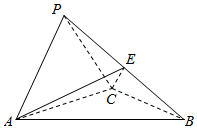 (Ⅰ)证明:如图,在△ACB中
(Ⅰ)证明:如图,在△ACB中
∵AC=BC=2,AB=2$\sqrt{2}$,∴AC2+BC2=AB2,则AC⊥BC,
又侧面PAC⊥底面ABC,∴BC⊥面PAC,则BC⊥PA,
又AP⊥PB,且PB∩BC=B,
∴PA⊥面PBC,则AP⊥PC;
(Ⅱ)解:在Rt△PCB中,由PC=1,BC=2,
可得${S}_{△PBC}=\frac{1}{2}×1×2=1$,
∵E为PB边的中点,∴${S}_{△PEC}=\frac{1}{2}{S}_{△PBC}=\frac{1}{2}$,
在Rt△APC中,
由PC=1,AC=2,得$PA=\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}$.
∴${V}_{A-PEC}=\frac{1}{3}×\frac{1}{2}×PA$=$\frac{\sqrt{3}}{6}$.
点评 本题考查平面与平面垂直的判定,考查了三棱锥体积的求法,考查空间想象能力和思维能力,是中档题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:选择题
一直三棱柱的每条棱长都是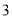 ,且每个顶点都在球
,且每个顶点都在球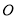 的表面上,则球
的表面上,则球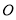 的半径为( )
的半径为( )
A.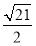 B.
B.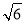 C.
C.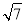 D.
D.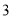
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:选择题
某四面体的三视图如图所示,则该四面体的四个面中,直角三角形的面积和是( )
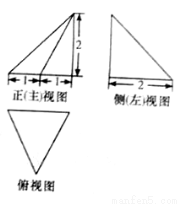
A. B.
B. C.
C.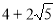 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
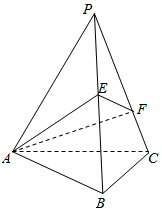 如图,已知正三棱锥P-ABC的底面边长为4,侧棱长为8,E、F分别为PB、PC上的动点,求截面△AEF周长的最小值,并求出此时三棱锥P-AEF的体积.
如图,已知正三棱锥P-ABC的底面边长为4,侧棱长为8,E、F分别为PB、PC上的动点,求截面△AEF周长的最小值,并求出此时三棱锥P-AEF的体积.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{2}]$ | B. | $[\frac{1}{2},+∞)$ | C. | $(0,6+2\sqrt{7})$ | D. | $(0,6-2\sqrt{7})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com