
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AA1=AD=a,E为CD上任意一点.
(I)求证:B1E⊥AD1;
(Ⅱ)若CD= ![]() a,是否存在这样的E点,使得AD1与平面B1AE成45°的角?说明理由.
a,是否存在这样的E点,使得AD1与平面B1AE成45°的角?说明理由.
【答案】证明:(I)连接A1D,B1C,
∵AA1=AD,AA1∥AD,AA1⊥AD,
∴四边形AA1D1D是正方形,
∴AD1⊥A1D,
∵A1B1⊥平面AA1D1D,AD1平面AA1D1D,
∴A1B1⊥AD1 ,
又A1D平面A1B1CD,A1B1平面A1B1CD,A1B1∩A1D=A1 ,
∴AD1⊥平面A1B1CD,又B1E平面A1B1CD,
∴B1E⊥AD1 .
(II)以A为原点,以AB,AD,AA1为坐标轴建立空间坐标系,
则A(0,0,0),D1(0,a,a),B1( ![]() a,0,a),设E(m,a,0),(0
a,0,a),设E(m,a,0),(0 ![]() ).
).
∴ ![]() =(0,a,a),
=(0,a,a), ![]() =(
=( ![]() a,0,a),
a,0,a), ![]() =(m,a,0).
=(m,a,0).
设平面B1AE的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 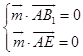 ,
,
∴ 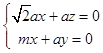 ,令x=1得
,令x=1得 ![]() =(1,﹣
=(1,﹣ ![]() ,﹣
,﹣ ![]() ).
).
∴cos< ![]() >=
>= 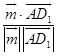 =﹣
=﹣ 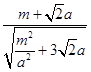 =﹣
=﹣ ![]() .
.
假设存在这样的E点,使得AD1与平面B1AE成45°的角,
则 ![]() =
= ![]() ,解得m=
,解得m= ![]() a.
a.
∴CD上存在点E使得AD1与平面B1AE成45°的角.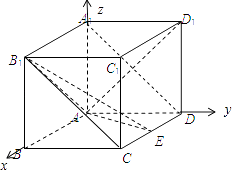
【解析】(I)连接A1D,B1C,则可通过证明AD1⊥平面A1B1CD得出B1E⊥AD1 . (II)以A为原点建立坐标系,设DE=m,求出 ![]() 及平面B1AE的法向量
及平面B1AE的法向量 ![]() ,令|cos<
,令|cos< ![]() >|=
>|= ![]() 解出m,根据m的值得出结论.
解出m,根据m的值得出结论.
【考点精析】利用空间中直线与直线之间的位置关系和空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知椭圆![]() :
:![]() 的左、右顶点分别为A,B,其离心率
的左、右顶点分别为A,B,其离心率![]() ,点
,点![]() 为椭圆上的一个动点,
为椭圆上的一个动点,![]() 面积的最大值是
面积的最大值是![]() .
.
(1)求椭圆的方程;
(2)若过椭圆![]() 右顶点
右顶点![]() 的直线
的直线![]() 与椭圆的另一个交点为
与椭圆的另一个交点为![]() ,线段
,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】连续抛掷同一颗均匀的骰子,令第i次得到的点数为ai , 若存在正整数k,使a1+a2+…+ak=6,则称k为你的幸运数字.
(1)求你的幸运数字为3的概率;
(2)若k=1,则你的得分为5分;若k=2,则你的得分为3分;若k=3,则你的得分为1分;若抛掷三次还没找到你的幸运数字则记0分,求得分X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,若椭圆经过点
,若椭圆经过点![]() ,且
,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设斜率为![]() 的直线
的直线![]() 与以原点为圆心,半径为
与以原点为圆心,半径为![]() 的圆交于
的圆交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,当
,当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() ,过
,过![]() 作与
作与![]() 轴垂直的直线与椭圆交于
轴垂直的直线与椭圆交于![]() 两点,
两点,![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 的斜率存在且不为0,直线
的斜率存在且不为0,直线![]() 交椭圆于
交椭圆于![]() 两点,若
两点,若![]() 中点为
中点为![]() ,
,![]() 为原点,直线
为原点,直线![]() 交
交![]() 于点
于点![]() ,若以
,若以![]() 为直径的圆过右焦点
为直径的圆过右焦点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() (a>b>0)的图象是曲线C.
(a>b>0)的图象是曲线C. 
(1)在如图的坐标系中分别做出曲线C的示意图,并分别标出曲线C与x轴的左、右交点A1 , A2 .
(2)设P是曲线C上位于第一象限的任意一点,过A2作A2R⊥A1P于R,设A2R与曲线C交于Q,求直线PQ斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
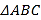
(1)设AD=x(x≥1),ED=y,求用x表示y的函数关系式;
(2)如果DE是灌溉水管,为节约成本,希望它最短,DE的位置应在哪里?如果DE是参观线路,则希望它最长,DE的位置又应在哪里?请予证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() =1(a>b>0)的左、右焦点分别为F1,F2,P是椭圆上一点,|PF1|=λ|PF2|
=1(a>b>0)的左、右焦点分别为F1,F2,P是椭圆上一点,|PF1|=λ|PF2|![]() ,∠F1PF2=
,∠F1PF2=![]() ,则椭圆离心率的取值范围为( )
,则椭圆离心率的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设常数a≥0,函数f(x)=x﹣ln2x+2alnx﹣1
(1)令g(x)=xf'(x)(x>0),求g(x)的最小值,并比较g(x)的最小值与0的大小;
(2)求证:f(x)在(0,+∞)上是增函数;
(3)求证:当x>1时,恒有x>ln2x﹣2alnx+1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com