
���� ��1���衰��������Ԫ���������������ֱ��Ϊ�¼�A��B��C����P��A��=$\frac{1}{2}$��P��B��=$\frac{1}{2}$��P��C��=$\frac{2}{3}$�������⣬���ɵ�·E��Ҫά�����������Σ���3��Ԫ��������������������3��Ԫ��2�����������������ɴ���������ɵ�·E��Ҫά�ĸ��ʣ�
��2��������֪X�Ŀ���ȡֵΪ0��100��200���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�E��X����
��� ����С��12�֣�
�⣺��1���衰��������Ԫ���������������ֱ��Ϊ�¼�A��B��C��
��P��A��=$\frac{1}{2}$��P��B��=$\frac{1}{2}$��P��C��=$\frac{2}{3}$��
�����⣬���ɵ�·E��Ҫά�����������Σ�
��3��Ԫ����������������������Ϊ��
p1=P��$\bar A\bar B\bar C$��=P��$\bar A$��+P��$\bar B$��+P��$\bar C$��=$\frac{1}{2}��\frac{1}{2}��\frac{2}{3}=\frac{1}{12}$��
��3��Ԫ��2��������������������Ϊ
p2=P��$A\bar B\bar C$��+P��$\bar AB\bar C$��+P��$\bar A\bar BC$��=$\frac{1}{2}��\frac{1}{2}��\frac{1}{3}$+$\frac{1}{2}��\frac{1}{2}��\frac{1}{3}$+$\frac{1}{2}��\frac{1}{2}��\frac{2}{3}$=$\frac{1}{3}$��
���ԣ����ɵ�·E��Ҫά�ĸ���Ϊp1+p2=$\frac{1}{12}$+$\frac{1}{3}$=$\frac{5}{12}$��
��2��������֪X�Ŀ���ȡֵΪ0��100��200��
P��X=0��=��1-$\frac{5}{12}$��2=$\frac{49}{144}$��
P��X=100��=$C_2^1$•$\frac{5}{12}$•��1-$\frac{5}{12}$��=$\frac{70}{144}$��
P��X=200��=��$\frac{5}{12}$��2=$\frac{25}{144}$��
X�ķֲ���Ϊ��
| X | 0 | 100 | 200 |
| P | $\frac{49}{144}$ | $\frac{70}{144}$ | $\frac{25}{144}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��к���ѧ������������������֤������������������������������˼�롢ת������˼�롢����˼�룬���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 8 | C�� | $\frac{4}{3}$ | D�� | $\frac{8}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 20 | B�� | 40 | C�� | 60 | D�� | 80 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
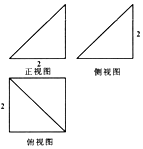
 ��ͼ��һ��������������ֽ�ϵ�����ͼ���������С������DZ߳�Ϊ1��С�����Σ���ü���������Ϊ��������
��ͼ��һ��������������ֽ�ϵ�����ͼ���������С������DZ߳�Ϊ1��С�����Σ���ü���������Ϊ��������| A�� | 6 | B�� | 8 | C�� | 12 | D�� | 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com