下列说法:①将一组数据中的每一个数据都加上或减去同一个常数后.方差不变,②设一个线性回归方程$\hat y=3-5x$.变量x增加1个单位时.y平均减少5个单位,③设具有相关关系的两个变量x.y的相关系数为r.则|r|越接近于0.x和y之间的线性相关程度越强,④在一个2×2列联表中.由计算得K2的值.则K2的值越大.判断两个变量间有关联的把握就� 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

4．下列说法：
①将一组数据中的每一个数据都加上或减去同一个常数后，方差不变；
②设一个线性回归方程$\hat y=3-5x$，变量x增加1个单位时，y平均减少5个单位；
③设具有相关关系的两个变量x，y的相关系数为r，则|r|越接近于0，x和y之间的线性相关程度越强；
④在一个2×2列联表中，由计算得K²的值，则K²的值越大，判断两个变量间有关联的把握就越大．其中错误的个数是（　　）

A．

B．

C．

D．

分析由一组数据中的每一个数据都加上或减去同一个常数后，方差不变判断①；利用回归方程的意义判断②；根据具有相关关系的两个变量的相关系数值与相关性判断③；由独立性检验中K²的值越大，判断两个变量间有关联的把握就越大判断④．

解答解：对于①，根据方差公式，将一组数据中的每一个数据都加上或减去同一个常数后，方差不变，故①正确；
对于②，设一个线性回归方程$\hat y=3-5x$，变量x增加1个单位时，y平均减少5个单位，故②正确；
对于③，设具有相关关系的两个变量x，y的相关系数为r，则|r|越接近于0，x和y之间的线性相关程度越弱，故③错误；
对于④，在一个2×2列联表中，由计算得K²的值，则K²的值越大，判断两个变量间有关联的把握就越大，故④正确．
∴其中错误的个数是1个．
故选：C．

点评本题考查命题的真假判断与应用，考查了变量间的相关关系，熟记教材结论是关键，是基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

18．已知圆（x+2）²+（y-2）²=a截直线x+y+2=0所得弦长为6，则实数a的值为11．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

15．命题“?x＜0，2^x＞0”的否定是（　　）

A．

?x＜0，2^x≤0

B．

?x＞0，2^x≤0

C．

?x＜0，2^x＞0

D．

?x＜0，2^x≤0

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

12．

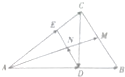如图所示，在△ABC中，3$\overrightarrow{AD}=2\overrightarrow{AB}$，3$\overrightarrow{AE}=2\overrightarrow{AC}$，AM是BC边上的中线，且交DE于N，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$．
（1）用$\overrightarrow{a}$，$\overrightarrow{b}$分别表示向量$\overrightarrow{DN}$，$\overrightarrow{AM}$；
（2）设∠BAC=θ，tanθ=$\sqrt{15}$，$\overrightarrow{a}$，$\overrightarrow{b}$均为单位向量，求$\overrightarrow{CD}$$•\overrightarrow{AM}$的值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

19．已知动圆过定点F（1，0），且与定直线1：x=-1相切．
（I）求动圆圆心的轨迹C的方程．
（Ⅱ）过点F作直线交轨迹C于A，B两点，O为坐标原点，若直线AO，BO分别交直线l₁：y=x+2于M，N两点，求△0MN面积的最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

9．已知函数f（x）=$\sqrt{3}$sin2ωx-2sin²ωx的最小正周期为3π．
（1）求函数f（x）的解析式；
（2）在△ABC中，若f（C）=1，AB=2，2sin²B=cosB+cos（A-C），求BC的长．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

16．已知集合A={sin0，cosπ}，B={x|x²-1=0}，则A∩B=（　　）

A．

{1，0，-1}

B．