
若函数h(x)满足
(1)h(0)=1,h(1)=0;
(2)对任意 ,有h(h(a))=a;
,有h(h(a))=a;
(3)在(0,1)上单调递减。则称h(x)为补函数。已知函数
(1)判函数h(x)是否为补函数,并证明你的结论;
(2)若存在 ,使得h(m)=m,若m是函数h(x)的中介元,记
,使得h(m)=m,若m是函数h(x)的中介元,记 时h(x)的中介元为xn,且
时h(x)的中介元为xn,且 ,若对任意的
,若对任意的 ,都有Sn<
,都有Sn<  ,求
,求 的取值范围;
的取值范围;
(3)当 =0,
=0, 时,函数y= h(x)的图像总在直线y=1-x的上方,求P的取值范围。
时,函数y= h(x)的图像总在直线y=1-x的上方,求P的取值范围。
见解析
【解析】(1)函数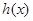 是补函数。证明如下:
是补函数。证明如下:
①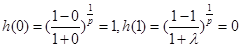 ;
;
②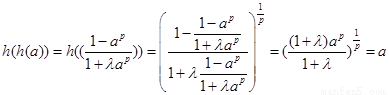 ;
;
③令 ,有
,有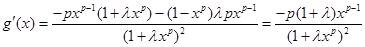 ,
,
因为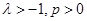 ,所以当
,所以当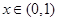 时,
时,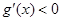 ,所以
,所以 在(0,1)上单调递减,故函数
在(0,1)上单调递减,故函数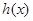 在(0,1)上单调递减。
在(0,1)上单调递减。
(2) 当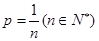 ,由
,由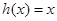 ,得:
,得: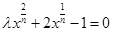
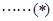
①当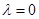 时,中介元
时,中介元 ;
;
②当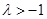 且
且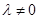 时,由(*)可得
时,由(*)可得 或
或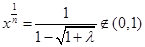 ;
;
得中介元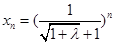 ,综上有对任意的
,综上有对任意的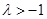 ,中介元
,中介元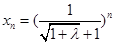 (
(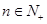 )
)
于是,当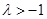 时,有
时,有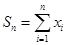 =
=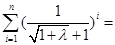
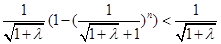
当n无限增大时, 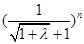 无限接近于,
无限接近于,
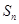 无限接近于
无限接近于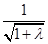 ,故对任意的
,故对任意的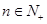 ,
,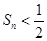 成立等价于
成立等价于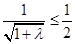 ,即
,即
 ;
;
(3) 当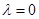 时,
时,
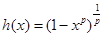 ,中介元是
,中介元是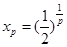
①当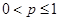 时,
时, 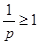 ,中介元为
,中介元为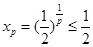 ,所以点
,所以点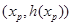 不在直线y=1-x的上方,不符合条件;
不在直线y=1-x的上方,不符合条件;
②当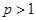 时,依题意只须
时,依题意只须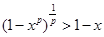 在
在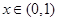 时恒成立,也即
时恒成立,也即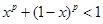 在
在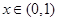 时恒成立,设
时恒成立,设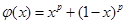 ,
,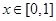 ,则
,则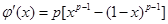 ,
,
由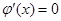 可得
可得 ,且当
,且当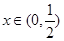 时,
时,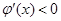 ,当
,当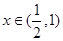 时,
时,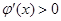 ,又因为
,又因为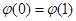 =1,所以当
=1,所以当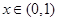 时,
时, 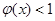 恒成立。
恒成立。
综上:p的取值范围为(1,+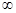 )。
)。
【点评】本题考查导数的应用、函数的新定义,函数与不等式的综合应用以及分类讨论,数形结合的数学思想. 高考中,导数解答题一般有以下几种考查方向:一、导数的几何意义,求函数的单调区间;二、用导数研究函数的极值,最值;三、用导数求最值的方法证明不等式.来年需要注意用导数研究函数最值的考查.


科目:高中数学 来源: 题型:
| a |
| 2 |
| b |
| 2 |
| 2 |
| x |
| x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x+y |
| 1+xy |
| 1-x |
| 1+x |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 4 |
| x |
| x | … | -3 | -2.3 | -2.2 | -2.1 | -2 | -1.9 | -1.7 | -1.5 | -1 | -0.5 | … |
| y | … | -4.3 | -4.04 | -4.02 | -4.005 | -4 | -4.005 | -4.05 | -4.17 | -5 | -8.5 | … |
| 4 |
| x |
| 4 |
| x |
| x2-ax+4 |
| x |
查看答案和解析>>
科目:高中数学 来源:2012年普通高等学校招生全国统一考试江西卷数学理科 题型:044
若函数h(x)满足
(1)h(0)=1,h(1)=0;
(2)对任意a∈[0,1],有h(h(a))=a;
(3)在(0,1)上单调递减.
则称h(x)为补函数.已知函数h(x)=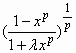 (λ>-1,p>0)
(λ>-1,p>0)
(1)判函数h(x)是否为补函数,并证明你的结论;
(2)若存在m∈[0,1],使得h(m)=m,若m是函数h(x)的中介元,记p=![]() (n∈N+)时h(x)的中介元为xn,且Sn=
(n∈N+)时h(x)的中介元为xn,且Sn=![]() ,若对任意的n∈N+,都有Sn<
,若对任意的n∈N+,都有Sn<![]() ,求λ的取值范围;
,求λ的取值范围;
(3)当λ=0,x∈(0,1)时,函数y=h(x)的图像总在直线y=1-x的上方,求P的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com