函数f(x)定义在区间[a,b]上,设“min{f(x)|x∈D}”表示函数f(x)在集合D上的最小值,“max{f(x)|x∈D}”表示函数f(x)在集合D上的最大值.现设f1(x)=min{f(t)|a≤t≤x}(x∈[a,b]),f2(x)=max{f(t)|a≤t≤x}(x∈[a,b]),
若存在最小正整数k,使得f2(x)-f1(x)≤k(x-a)对任意的x∈[a,b]成立,则称函数f(x)为区间[a,b]上的“第k类压缩函数”.
(Ⅰ) 若函数f(x)=x3-3x2,x∈[0,3],求f(x)的最大值,写出f1(x),f2(x)的解析式;
(Ⅱ) 若m>0,函数f(x)=x3-mx2是[0,m]上的“第3类压缩函数”,求m的取值范围.
【答案】
分析:(I)求出导函数,令导函数大于0求出x的范围即为递增区间;令导函数小于0求出x的范围即为递减区间,利用f
1(x),f
2(x)的定义,求出它们的解析式.
(II)求出函数f(x)=x
3-mx
2的导函数,通过导数判断出其单调性,得到f
1(x),f
2(x)的解析式,根据“第3类压缩函数”的定义列出不等式,求出m的范围.
解答:解:(Ⅰ)由于f'(x)=3x
2-6x,
令f'(x)=3x
2-6x>0得2<x<3;f'(x)=3x
2-6x<0得0<x<2
故f(x)在[0,2]上单调递减,在[2,3]上单调递增.
所以,f(x)的最大值为max{f(0),f(3)}=0.…(3分)

,…(6分)
f
2(x)=0,…(9分)
(Ⅱ)由于f'(x)=3x
2-2mx,
故f(x)在

上单调递减,在
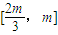
上单调递增,
而f(0)=f(m)=0,

,
故
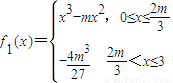
,f
2(x)=0,
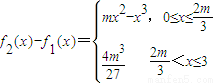
.…(11分)
设对正整数k有f
2(x)-f
1(x)≤kx对x∈[0,m]恒成立,
当x=0时,k∈N
*均成立;
当
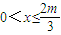
时,
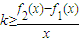
恒成立,
而
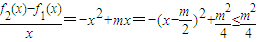
,
故
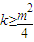
;
当

时,

恒成立,
而
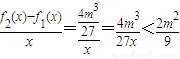
;
故
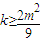
;
所以,
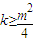
,
又f(x)是[0,m]上的“第3类压缩函数”,
故
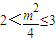
,
所以,

.…(14分)
点评:本题主要考查学生的对新问题的接受、分析和解决的能力.要求学生要有很扎实的基本功才能作对这类问题.

 ,…(6分)
,…(6分) 上单调递减,在
上单调递减,在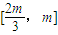 上单调递增,
上单调递增, ,
,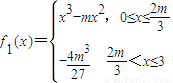 ,f2(x)=0,
,f2(x)=0,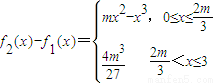 .…(11分)
.…(11分)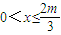 时,
时,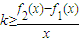 恒成立,
恒成立,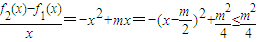 ,
,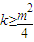 ;
; 时,
时, 恒成立,
恒成立,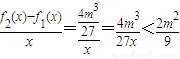 ;
;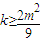 ;
;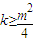 ,
,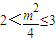 ,
, .…(14分)
.…(14分)

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案