
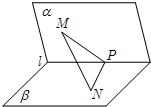
 如图,α-l-β为60°的二面角,等腰直角三角形MPN的直角顶点P在l上,M∈α,N∈β,且MP和NP与l所成的角相等,则MN与β所成角为
如图,α-l-β为60°的二面角,等腰直角三角形MPN的直角顶点P在l上,M∈α,N∈β,且MP和NP与l所成的角相等,则MN与β所成角为| 2 |
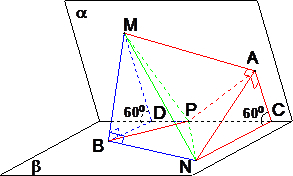 解:作NA⊥α于A,MB⊥β于B,连接AP、PB、BN、AM,
解:作NA⊥α于A,MB⊥β于B,连接AP、PB、BN、AM,| 2 |
| 2 |
| 2 |
| ||
| 3 |
| ||
| 3 |
| MB |
| 6sin60° |
2
| ||
| 3 |
| PC |
| PN |
| BD |
| PB |
| ||
| a |
| DB | ||
|
| ||||||
| a |
| ||||
3
|
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
2
| ||
| 3 |
| 2 |
| 1 |
| 2 |


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
 如图直线l与x轴、y轴的正半轴分别交于A(8,0)、B(0,6)两点,P为直线l上异于A、B两点之间的一动点.且PQ∥OA交OB于点Q.
如图直线l与x轴、y轴的正半轴分别交于A(8,0)、B(0,6)两点,P为直线l上异于A、B两点之间的一动点.且PQ∥OA交OB于点Q.查看答案和解析>>
科目:高中数学 来源: 题型:
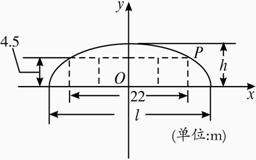
(1)若最大拱高h为6 m,则隧道设计的拱宽l是多少?
(2)若最大拱高h不小于6 m,则应如何设计拱高h和拱宽l,才能使半个椭圆形隧道的土方工程量最小?(半个椭圆的面积公式为![]() lh,柱体体积为底面积乘以高.结果精确到0.1 m)
lh,柱体体积为底面积乘以高.结果精确到0.1 m)
查看答案和解析>>
科目:高中数学 来源: 题型:
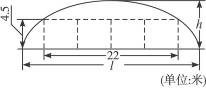
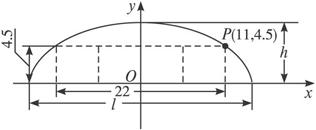
如图,某隧道设计为双向四车道,车道总宽22米,要求通过车辆限高4.5米,隧道全长2.5千米,隧道的拱线近似地看成半个椭圆形状.
(1)若最大拱高h为6米,则隧道设计的拱宽l是多少?
(2)若最大拱高h不小于6米,则应如何设计拱高h和拱宽l,才能使半个椭圆形隧道的土方工程量最小?
(半个椭圆的面积公式为S=![]() lh,柱体体积为:底面积乘以高.本题结果均精确到0.1米)
lh,柱体体积为:底面积乘以高.本题结果均精确到0.1米)
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)若最大拱高h为6米,则隧道设计的拱宽l是多少?
(2)若最大拱高h不小于6米,则应如何设计拱高h和拱宽l,才能使半个椭圆形隧道的土方工程量最小?
(半个椭圆的面积公式为S=![]() lh,柱体体积为:底面积乘以高.本题结果均精确到0.1米)
lh,柱体体积为:底面积乘以高.本题结果均精确到0.1米)
查看答案和解析>>
科目:高中数学 来源:2012-2013学年宁夏银川一中高一(上)期末数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com