
分析 设圆心C(2b+1,b),根据题意可得|CO|=|CA|=r,由此求得b的值,可得圆心坐标和半径,从而得到所求圆的标准方程.
解答 解:设圆心C(2b+1,b),半径为r,再根据圆过原点和点A(1,2),
可得|CO|=|CA|=r,∴(2b+1)2+b2=(2b+1-1)2+(b-2)2,
求得b=$\frac{3}{8}$,可得圆心C($\frac{7}{4}$,$\frac{3}{8}$),半径${r}^{2}=|OC{|}^{2}=\frac{205}{64}$.
∴圆C的标准方程为$(x-\frac{7}{4})^{2}+(y-\frac{3}{8})^{2}=\frac{205}{64}$.
点评 本题主要考查求圆的标准方程的方法,求出圆心坐标和半径的值,是解题的关键,属于基础题.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 正方体的体积与棱长的关系 | |
| B. | 学生的成绩和体重 | |
| C. | 路上酒后驾驶的人数和交通事故发生的多少 | |
| D. | 水的体积和重量 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
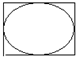 矩形长为6,宽为4,在矩形内随机地撒300粒黄豆,数得落在椭圆外的黄豆数为66颗,以此实验数据为依据可以估算出椭圆的面积为( )
矩形长为6,宽为4,在矩形内随机地撒300粒黄豆,数得落在椭圆外的黄豆数为66颗,以此实验数据为依据可以估算出椭圆的面积为( )| A. | 5.28 | B. | 16.32 | C. | 17.28 | D. | 18.72 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com