
【题目】设![]() 为实数,已知函数
为实数,已知函数![]() 的导函数为
的导函数为![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)设![]() 为实数,若对于任意
为实数,若对于任意![]() ,不等式
,不等式![]() 恒成立,且存在唯一的实数
恒成立,且存在唯一的实数![]() 使得
使得![]() 成立,求
成立,求![]() 的值;
的值;
(3)是否存在负数![]() ,使得
,使得![]() 是曲线
是曲线![]() 的切线.若存在,求出
的切线.若存在,求出![]() 的所有值:若不存在,请说明理由.
的所有值:若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)求出![]() ,再由
,再由![]() ,即可求出
,即可求出![]() 值;
值;
(2)由(1)的结论将问题转化为![]() 恒成立,设
恒成立,设![]() ,即为
,即为![]() ,通过导数法求出
,通过导数法求出![]() ,求出
,求出![]() 的取值范围,再由
的取值范围,再由![]() 唯一解,求出
唯一解,求出![]() 的值;
的值;
(3)设切点的横坐标为![]() ,求出切线斜率,结合已知得
,求出切线斜率,结合已知得![]() ,将切点坐标代入
,将切点坐标代入![]() ,整理得到关于
,整理得到关于![]() 的方程
的方程![]() ,转化为关于
,转化为关于![]() 的方程正数解的情况,即为
的方程正数解的情况,即为![]() 与直线
与直线![]() 在第一象限交点情况,通过求导,求出
在第一象限交点情况,通过求导,求出![]() 单调区间,以及最值,即可求解.
单调区间,以及最值,即可求解.
(1)因为![]() ,
,
所以![]() ,
,
故![]() .
.
(2)因为![]() ,
,
所以![]() 恒成立.
恒成立.
记![]() ,
,
则![]() ,
,
因为![]() ,且
,且![]() ,
,
所以![]() ,
,
因此为![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
所以![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,
,
故方程![]() 无解,
无解,
当![]() 时,当
时,当![]() 时,由单调性知
时,由单调性知![]()
所以存在唯一的![]() 使得
使得![]() ,即
,即![]() .
.
(3)设切点的横坐标为![]() ,则
,则
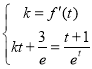 ,即
,即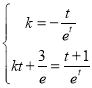 ,
,
![]() ,即
,即![]()
原命题等价于存在正数![]() 使得方程
使得方程![]() 成立.
成立.
记![]() ,
,
则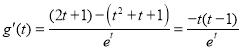 ,
,
令![]() ,则
,则![]() ,
,
因此当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,![]() ;
;
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,![]() ,
,
则![]() .
.
故存在唯一的正数![]() 使得方程
使得方程![]() 成立,
成立,
即存在唯一的负数![]() ,
,
使得![]() 是曲线
是曲线![]() 的切线.
的切线.


科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 同时满足以下条件:①
同时满足以下条件:①![]() 在
在![]() 上为减函数,
上为减函数,![]() 上是增函数;②
上是增函数;②![]() 是偶函数;③
是偶函数;③![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(1)求函数![]() 的解析式;
的解析式;
(2)设![]() ,若对
,若对![]()
![]() ,使
,使![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数为( )
①“![]() 为真”是“
为真”是“![]() 为真”的充分不必要条件;
为真”的充分不必要条件;
②若数据![]() 的平均数为1,则
的平均数为1,则![]() 的平均数为2;
的平均数为2;
③在区间![]() 上随机取一个数
上随机取一个数![]() ,则事件“
,则事件“![]() ”发生的概率为
”发生的概率为![]()
④已知随机变量![]() 服从正态分布
服从正态分布![]() ,且
,且![]() ,则
,则![]() .
.
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从抛物线![]() 上任意一点P向x轴作垂线段,垂足为Q,点M是线段
上任意一点P向x轴作垂线段,垂足为Q,点M是线段![]() 上的一点,且满足
上的一点,且满足![]()
(1)求点M的轨迹C的方程;
(2)设直线![]() 与轨迹c交于
与轨迹c交于![]() 两点,T为C上异于
两点,T为C上异于![]() 的任意一点,直线
的任意一点,直线![]() ,
,![]() 分别与直线
分别与直线![]() 交于
交于![]() 两点,以
两点,以![]() 为直径的圆是否过x轴上的定点?若过定点,求出符合条件的定点坐标;若不过定点,请说明理由.
为直径的圆是否过x轴上的定点?若过定点,求出符合条件的定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明.下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实.图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实、黄实,利用![]() ,化简,得
,化简,得![]() .设勾股形中勾股比为
.设勾股形中勾股比为![]() ,若向弦图内随机抛掷
,若向弦图内随机抛掷![]() 颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
①已知随机变量![]() 服从正态分布
服从正态分布![]() ,且
,且![]() ,则
,则![]() ;
;
②相关系数r用来衡量两个变量之间线性关系的强弱,![]() 越大,相关性越弱;
越大,相关性越弱;
③相关指数![]() 用来刻画回归的效果,
用来刻画回归的效果,![]() 越小,说明模型的拟合效果越好;
越小,说明模型的拟合效果越好;
④在残差图中,残差点分布的带状区域越狭窄,其模型拟合的精度就越高.
A.①②B.①④C.②③D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为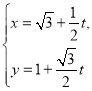 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程及曲线
的极坐标方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 是直线
是直线![]() 上一点,
上一点,![]() 是曲线
是曲线![]() 上一点,求
上一点,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com