
| OM |
| OC |
| ||
|
|
| ||
|
|
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
 (2012•九江一模)已知点G是△ABC的外心,
(2012•九江一模)已知点G是△ABC的外心,| GA |
| GB |
| GC |
| GA |
| AB |
| AC |
| 0 |
| GA |
| AB |
| OA |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点G是△ABC的外心,![]() 是三个单位向量,且满足2
是三个单位向量,且满足2![]() ,|
,|![]() |=|
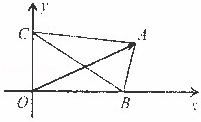
|=|![]() |.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则|
|.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则|![]() |的最大值为 .
|的最大值为 .
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省南昌十九中高三(上)第四次月考数学试卷(理科)(解析版) 题型:填空题
 是三个单位向量,且满足2
是三个单位向量,且满足2 ,|
,| |=|
|=|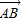 |.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则|
|.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则| |的最大值为 .
|的最大值为 .
查看答案和解析>>
科目:高中数学 来源:2012年江西省九江市高考数学一模试卷(文科)(解析版) 题型:解答题
 是三个单位向量,且满足2
是三个单位向量,且满足2 ,|
,| |=|
|=| |.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则|
|.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则| |的最大值为 .
|的最大值为 .
查看答案和解析>>
科目:高中数学 来源:2012年江西省九江市高考数学一模试卷(理科)(解析版) 题型:解答题
 是三个单位向量,且满足2
是三个单位向量,且满足2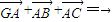 ,|
,| |=|
|=| |.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则|
|.如图所示,△ABC的顶点B、C分别在x轴和y轴的非负半轴上移动,O是坐标原点,则| |的最大值为 .
|的最大值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com