
已知i,m,n是正整数,且1<i≤m<n.
(1)证明: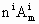 <
<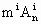 ;
;
(2)证明:(1+m)n>(1+n)m.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
|
|
| 7 |
| 4 |
| x2 |
| 16 |
| y2 |
| 5 |
| z2 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 1 |
| 2 |
| 5 |
| 6 |
查看答案和解析>>
科目:高中数学 来源:2004年高考教材全程总复习试卷·数学 题型:044
已知全集I={1,2,3,4,5,6,7,8},集合A={1,2,3,4,5},B={1,2,3,4,7,8},从A∩B和(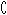 IA)∪(
IA)∪(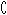 IB)中各取两个数字.
IB)中各取两个数字.
(1)能组成多少个比6100大的四位数.
(2)能组成多少个被5除余2的四位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com