A
分析:令f(x)=x
3+2011x-1,,由f′(x)=3x
2+2011>0可得f(x)在R上单调递增且连续的函数,结合零点判定及f(0),f(1)的符号可知函数f(x)=x
3+2011x-1只有唯一的零点x
0∈(0,1)从而可得a
5-1,的符号,同理可得a
2007-1的符号,由已知两式相加可得,(a
5+a
2007-2)[(a
5-1)
2+(a
2007-1)
2-(a
5-1)(a
2007-1)+2011]=0,从而有a
5+a
2007-2=0,由等差数列的性质可得a
1+a
2011=a
5+a
2007=2,代入等差数列的求和公式
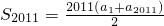
可求
解答:令f(x)=x
3+2011x-1,g(x)=x
3+2011x+1
f′(x)=3x
2+2011>0
f(x)在R上单调递增且连续的函数
f(0)=-1<0,f(1)=2011>0
函数f(x)=x
3+2011x-1只有唯一的零点x
0∈(0,1)
从而可得0<a
5-1<1,1<a
5<2,-1<a
2007<0∴a
2007<a
5∵(a
5-1)
3+2011(a
5-1)=1,(a
2007-1)
3+2011(a
2007-1)=-1
两式相加整理可得,(a
5+a
2007-2)[(a
5-1)
2+(a
2007-1)
2-(a
5-1)(a
2007-1)+2011]=0
由0<a
5-1<1,-1<a
2007-1<0可得(a
5-1)
2+(a
2007-1)
2-(a
5-1)(a
2007-1)+2011>0
∴a
5+a
2007-2=0
由等差数列的性质可得,a
1+a
2011=a
5+a
2007=2
∴
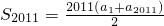
=2011
故选:A
点评:本题主要考查了利用函数的导数及单调性、由函数的性质判定零点的范围,等差数列性质(若m+n=p+q,则a
m+a
n=a
p+a
q)的应用及求和公式
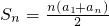
应用,本题是一道综合性非常好的试题,知识的应用也比较灵活.考试要注意体会应用.

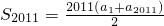 可求
可求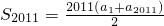 =2011
=2011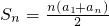 应用,本题是一道综合性非常好的试题,知识的应用也比较灵活.考试要注意体会应用.
应用,本题是一道综合性非常好的试题,知识的应用也比较灵活.考试要注意体会应用. 
