“开心辞典”中有这样的问题：给出一组数，要你根据规律填出后面的第几个数，现给出一组数：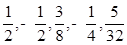
它的第8个数可以是 。
名校练考卷期末冲刺卷系列答案科目：高中数学 来源： 题型：填空题
在平面几何中有如下结论：若正三角形ABC的内切圆面积为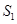
，外接圆面积为
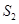，则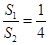
.推广到空间几何体中可以得到类似结论：若正四面体ABCD的内切球体积为
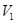，外接球体积为
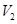，则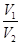
=___________.
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
（2013•湖北）古希腊毕达哥拉斯学派的数学家研究过各种多边形数，如三角形数1，3，6，10，…，第n个三角形数为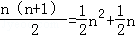
．记第n个k边形数为N（n，k）（k≥3），以下列出了部分k边形数中第n个数的表达式：
三角形数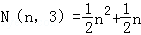
，
正方形数N（n，4）=n2，
五边形数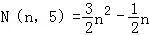
，
六边形数N（n，6）=2n2﹣n，
…
可以推测N（n，k）的表达式，由此计算N（10，24）= _________ ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，分母上是2的乘方，分子组成等差数列，奇数项符号为正，偶数项符号为负，通项公式可为an=（1）n+1•
，它的第8个数可以是an=
=
.
,
,
,
,…,由此你猜想出第n个数为 
是
则
_____________;
表示不超过
的最大整数，例如
，
.设函数
，当
时，函数
的值域为集合
，则
，根据上述规律，第五个等式为
.
…
…
，
的分解中最小的正整数是21，则
.