【答案】
分析:解法一:(Ⅰ)直接利用用数学归纳法证明的证明方法证明即可;
(Ⅱ)对于n≥6,已知
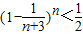
,利用指数函数的性质以及放缩法证
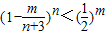
,m=1,2…,n;
(Ⅲ)利用(Ⅱ)的结论,以及验证n=1,2,3,4,5时等式是否成立,即可求出满足等式3
n+4
m+…+(n+2)
m=(n+3)
n的所有正整数n.
解法二::(Ⅰ)证:当x=0或m=1时,原不等式中等号显然成立,下用数学归纳法证明.
(Ⅱ)同解法一;
(Ⅲ)利用反证法证明当n≥6时,不存在满足该等式的正整数n.验证同解法一.
解答:解法1:(Ⅰ)证:用数学归纳法证明:
当x=0时,(1+x)
m≥1+mx;即1≥1成立,
x≠0时,证:用数学归纳法证明:
(ⅰ)当m=1时,原不等式成立;
当m=2时,左边=1+2x+x
2,右边=1+2x,
因为x
2≥0,所以左边≥右边,原不等式成立;
(ⅱ)假设当m=k时,不等式成立,即(1+x)
k≥1+kx,
则当m=k+1时,∵x>-1,
∴1+x>0,于是在不等式(1+x)
k≥1+kx两边同乘以1+x得
(1+x)
k•(1+x)≥(1+kx)(1+x)=1+(k+1)x+kx
2≥1+(k+1)x,
所以(1+x)
k+1≥1+(k+1)x.即当m=k+1时,不等式也成立.
综合(ⅰ)(ⅱ)知,对一切正整数m,不等式都成立.
(Ⅱ)证:当n≥6,m≤n时,由(Ⅰ)得
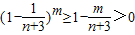
,
于是

=
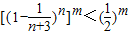
,m=1,2,n.
(Ⅲ)解:由(Ⅱ)知,当n≥6时,
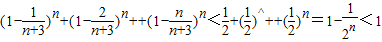
,∴
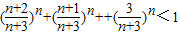
.
即3
n+4
n+…+(n+2)
n<(n+3)
n.即当n≥6时,不存在满足该等式的正整数n.
故只需要讨论n=1,2,3,4,5的情形:
当n=1时,3≠4,等式不成立;
当n=2时,3
2+4
2=5
2,等式成立;
当n=3时,3
3+4
3+5
3=6
3,等式成立;
当n=4时,3
4+4
4+5
4+6
4为偶数,而7
4为奇数,故3
4+4
4+5
4+6
4≠7
4,等式不成立;
当n=5时,同n=4的情形可分析出,等式不成立.
综上,所求的n只有n=2,3.
解法2:(Ⅰ)证:当x=0或m=1时,原不等式中等号显然成立,下用数学归纳法证明:
当x>-1,且x≠0时,m≥2,(1+x)
m>1+mx. ①
(ⅰ)当m=2时,左边=1+2x+x
2,右边=1+2x,因为x≠0,所以x
2>0,即左边>右边,不等式①成立;
(ⅱ)假设当m=k(k≥2)时,不等式①成立,即(1+x)
k>1+kx,则当m=k+1时,
因为x>-1,所以1+x>0.又因为x≠0,k≥2,所以kx
2>0.
于是在不等式(1+x)
k>1+kx两边同乘以1+x得(1+x)
k•(1+x)>(1+kx)(1+x)=1+(k+1)x+kx
2>1+(k+1)x,
所以(1+x)
k+1>1+(k+1)x.即当m=k+1时,不等式①也成立.
综上所述,所证不等式成立.
(Ⅱ)证:当n≥6,m≤n时,∵
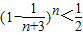
,
∴
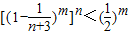
,
而由(Ⅰ),

,
∴
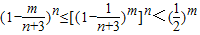
.
(Ⅲ)解:假设存在正整数n
≥6使等式
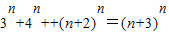
成立,
即有
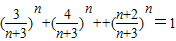
. ②
又由(Ⅱ)可得
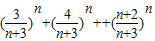
=
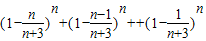
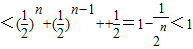
,与②式矛盾.
故当n≥6时,不存在满足该等式的正整数n.
下同解法1.
点评:本小题主要考查数学归纳法、数列求和、不等式等基础知识和基本的运算技能,考查分析问题能力和推理能力.注意放缩法的应用.

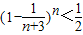 ,求证
,求证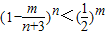 ,m=1,2…,n;
,m=1,2…,n;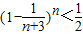 ,利用指数函数的性质以及放缩法证
,利用指数函数的性质以及放缩法证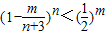 ,m=1,2…,n;
,m=1,2…,n;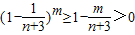 ,
, =
=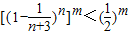 ,m=1,2,n.
,m=1,2,n.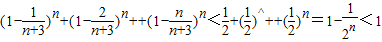 ,∴
,∴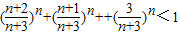 .
.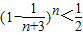 ,
,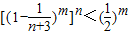 ,
, ,
,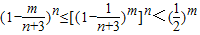 .
.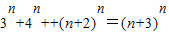 成立,
成立,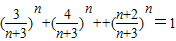 . ②
. ②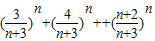
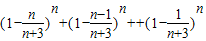
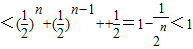 ,与②式矛盾.
,与②式矛盾.

![]() ,求证
,求证![]() ,m=1,1,2…,n;
,m=1,1,2…,n;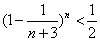 ,求证
,求证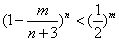 ,m=1,2,3,…,n;
,m=1,2,3,…,n;