
(本小题满分12分)下图是调查某地某公司1000名员工的月收入后制作的直方图.根据直方图估计: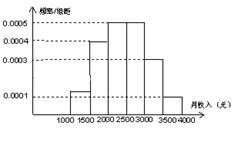
(Ⅰ)该公司月收入在1000元到1500元之间的人数;
(Ⅱ)该公司员工的月平均收入;
(Ⅲ)该公司员工收入的众数;
(Ⅳ)该公司员工月收入的中位数
(Ⅰ) 人;(Ⅱ)
人;(Ⅱ)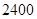 元;(Ⅲ)
元;(Ⅲ)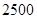 元;(Ⅳ)
元;(Ⅳ)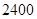 元.
元.
解析试题分析:(Ⅰ)直方图类的题,核心是要抓住频率之和为1,图中仅有欲求频率未知,所以用1减去其余各组频率之和即可,然后乘于总人数可得所求;(Ⅱ)由直方图求平均数只需用频率分布直方图各个小矩形的面积(即频率)乘底边中点的横坐标,然后求和可得;(Ⅲ)众数在频率分布直方图中,就是最高矩形的中点的横坐标;(Ⅳ)直方图中,中位数左边和右边的面积相等,都是0.5,据此易得所求.
试题解析:(Ⅰ)根据频率分布直方图知,满足条件的频率为: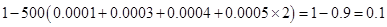 ,
,
所以满足条件的人数为: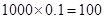 人;
人;
(Ⅱ)据题意该公司员工的平均收入为: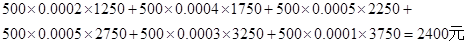
(Ⅲ)根据频率分布直方图知,最高矩形(由两个频率相同的矩形构成)的底边中点的横坐标为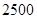 ,即公司员工收入的众数为
,即公司员工收入的众数为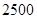 元;
元;
(Ⅳ)根据频率分布直方图知,中位数介于2000元至2500元之间,故可设中位数为 ,则由
,则由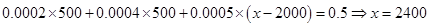 ,
,
即公司员工收入的中位数为2400元.
考点:①频率的定义和性质;②平均数、众数、中位数与频率直方图的关系.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:解答题
已知椭圆E: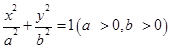 的离心率
的离心率 ,并且经过定点
,并且经过定点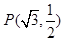
(1)求椭圆E 的方程;
(2)问是否存在直线y=-x+m,使直线与椭圆交于A, B 两点,满足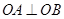 ,若存在求m 值,若不存在说明理由.
,若存在求m 值,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
将一个棱长为4 的立方体表面涂上红色后,再均匀分割成棱长为1
的立方体表面涂上红色后,再均匀分割成棱长为1 的小正方体.从涂有红色面的小正方体中随机取出一个小正方体,则这个小正方体表面的红色面积不少于2
的小正方体.从涂有红色面的小正方体中随机取出一个小正方体,则这个小正方体表面的红色面积不少于2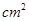 的概率是( )
的概率是( )
A. | B. | C.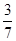 | D. 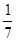 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com