练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知椭圆E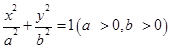：的离心率，并且经过定点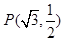
    （1）求椭圆E 的方程；
    （2）问是否存在直线y=-x+m，使直线与椭圆交于A, B 两点，满足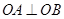,若存在求m 值，若不存在说明理由．

    （1）;（2）．

    解析试题分析：（1）利用椭圆E：的离心率，并且经过定点，建立方程，求出a，b，即可求椭圆E的方程；（2）直线y=-x+m代入椭圆方程，利用韦达定理，结合OA⊥OB⇒，即可求m值．
    试题解析：解（1）由题意：且，又
    解得：，即：椭圆E的方程为
    （2）设
        （*）
    所以

    由
    得
    又方程（*）要有两个不等实根，
    m的值符合上面条件，所以
    考点：直线与圆锥曲线的综合问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：单选题

    已知点在抛物线的准线上，过点的直线与在第一象限相切于点，记的焦点为，则的值为

    A．3 B．4 C．5 D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知双曲线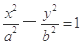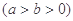的左焦点为F，过F作圆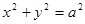的切线，切点为E，延长FE交双曲线右支于点P，若E为PF的中点，则双曲线的离心率为      （    ）

    A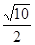． B．5 C．2 D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    方程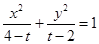所表示的曲线为C，有下列命题：
    ①若曲线C为椭圆，则；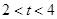
    ②若曲线C为双曲线，则或；
    ③曲线C不可能为圆；
    ④若曲线C表示焦点在上的双曲线，则。
    以上命题正确的是 __________ .（填上所有正确命题的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知中心在原点，对称轴为坐标轴，长半轴长与短半轴长的和为，离心率为的椭圆的标准方程为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知的取值如下表所示，若与线性相关，且，则（   ）











     
    A．         B．        C．      D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    某市对上下班交通情况作抽样调查，作出上下班时间各抽取 的12辆机动车行驶时速（单位：km/h）的茎叶图如图.则上、下班行驶时速的中位数分别为（）

    A．28与28.5B．29与28.5C．28与27.5 D．29与27.5

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知样本的平均数是，标准差是，则         

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）下图是调查某地某公司1000名员工的月收入后制作的直方图.根据直方图估计：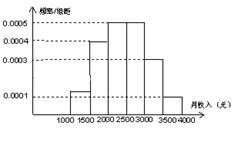

    （Ⅰ）该公司月收入在1000元到1500元之间的人数;
    （Ⅱ）该公司员工的月平均收入;
    （Ⅲ）该公司员工收入的众数;
    （Ⅳ）该公司员工月收入的中位数

    查看答案和解析>>

    同步练习册答案