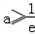练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设函数f（x）=（x+a）lnx﹣x+a．
    （Ⅰ）设g（x）=f'（x），求g（x）函数的单调区间；
    （Ⅱ）若，试研究函数f（x）=（x+a）lnx﹣x+a的零点个数．

    解：（Ⅰ）g（x）的定义域是（0，+∞）
    ∵g（x）=f'（x）=+lnx，
    ∴g'（x）=﹣，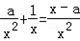
    （1）当a≤0时，g'（x）＞0，
    ∵g（x）在（0，+∞）上单调递增，故g（x）单调区间是（0，+∞）
    （2）当a＞0时，g'（x）＞0，
    ∵g（x）在（a，+∞）上单调递增，再由g'（x）＜0得g（x）在（0，a）上单调递减．
    g（x）的单调区间是（0，a）与（a，+∞）
    （Ⅱ）由题（Ⅰ）知，g（x）在x=a时取到最小值，且为g（a）=+lna=1+lna．
    ∵a≥，
    ∴lna≥﹣1，
    ∴g（a）≥0。
    ∴f'（x）≥g（a）≥0．f（x）在（0，+∞）上单调递增，
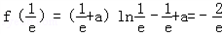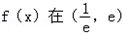    ∵f（e）=（e+a）lne﹣e+a=2a＞0，＜0，∴内有零点．
    故函数f（x）=（x+a）lnx﹣x+a的零点个数为1．

    练习册系列答案
  • 七彩题卡口算应用一点通系列答案
  • 课堂导学案湖南教育出版社系列答案
  • 轻巧夺A学业水平测试系列答案
  • 好学生小学口算题卡系列答案
  • 远航教育口算题卡系列答案
  • 扬帆文化100分培优智能优选卷系列答案
  • 多维互动提优课堂系列答案
  • 全效学习衔接教材系列答案
  • 巩固与提高郑州大学出版社系列答案
  • 金太阳导学测评系列答案
    • 年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设函数f（x）=a2x2（a＞0），g（x）=blnx．
    （1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为
    		2
    ，求a的值；
    （2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
    （3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
    		2
    2
    ，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数f（x）是定义在R上的偶函数，且f（x+2）=f（x）恒成立；当x∈[0，1]时，f（x）=x3-4x+3．有下列命题：
    ①f(-
    3
    4
    ) ＜f(
    15
    2
    )    ；
    ②当x∈[-1，0]时f（x）=x3+4x+3；
    ③f（x）（x≥0）的图象与x轴的交点的横坐标由小到大构成一个无穷等差数列；
    ④关于x的方程f（x）=|x|在x∈[-3，4]上有7个不同的根．
    其中真命题的个数为（　　）

    查看答案和解析>>

    科目：高中数学 来源：徐州模拟 题型：解答题

    设函数f（x）=a2x2（a＞0），g（x）=blnx．
    （1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为2
    		2
    ，求a的值；
    （2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
    （3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
    		2
    2
    ，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2011年江苏省苏、锡、常、镇四市高三调研数学试卷（一）（解析版） 题型：解答题

    设函数f（x）=x（x-1）2，x＞0．
    （1）求f（x）的极值；
    （2）设0＜a≤1，记f（x）在（0，a]上的最大值为F（a），求函数的最小值；
    （3）设函数g（x）=lnx-2x2+4x+t（t为常数），若使g（x）≤x+m≤f（x）在（0，+∞）上恒成立的实数m有且只有一个，求实数m和t的值．

    查看答案和解析>>

    科目：高中数学 来源：2011年江苏省苏州市高考数学一模试卷（解析版） 题型：解答题

    设函数f（x）=x（x-1）2，x＞0．
    （1）求f（x）的极值；
    （2）设0＜a≤1，记f（x）在（0，a]上的最大值为F（a），求函数的最小值；
    （3）设函数g（x）=lnx-2x2+4x+t（t为常数），若使g（x）≤x+m≤f（x）在（0，+∞）上恒成立的实数m有且只有一个，求实数m和t的值．

    查看答案和解析>>

    同步练习册答案