
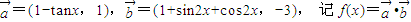
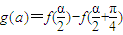 ,则求g(a)的最小值.
,则求g(a)的最小值. •
• 后,得到函数f(x)的解析式,第一项第一个括号中利用同角三角函数间的基本关系切化弦进行化简,第二个括号利用二倍角的正弦、余弦函数公式化简,约分后再利用二倍角的余弦函数公式化为一个角的余弦函数,找出ω的值,代入周期公式T=
后,得到函数f(x)的解析式,第一项第一个括号中利用同角三角函数间的基本关系切化弦进行化简,第二个括号利用二倍角的正弦、余弦函数公式化简,约分后再利用二倍角的余弦函数公式化为一个角的余弦函数,找出ω的值,代入周期公式T=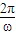 ,即可求出函数的最小正周期;
,即可求出函数的最小正周期; 和x=
和x= 分别代入得出的函数f(x)解析式,确定出g(α)的解析式,利用两角和与差的余弦函数公式化简后,再根据两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,由正弦函数的值域即可得到g(α)的最小值.
分别代入得出的函数f(x)解析式,确定出g(α)的解析式,利用两角和与差的余弦函数公式化简后,再根据两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,由正弦函数的值域即可得到g(α)的最小值.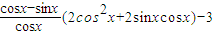
 =π;
=π;
 ,
, .
.

 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:解答题
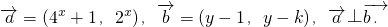
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆![]() ,坐标原点为O.圆C上任意一点A在x轴上的射影为点B,已知向量
,坐标原点为O.圆C上任意一点A在x轴上的射影为点B,已知向量![]() .
.
(1)求动点Q的轨迹E的方程;
(2)当![]() 时,设动点Q关于x轴的对称点为点P,直线PD交轨迹E于点F(异于P点),证明:直线QF与x轴交于定点,并求定点坐标.
时,设动点Q关于x轴的对称点为点P,直线PD交轨迹E于点F(异于P点),证明:直线QF与x轴交于定点,并求定点坐标.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省黄冈市罗田县育英高中高一(上)期末数学试卷(解析版) 题型:解答题
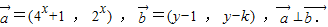
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省菏泽市鄄城职业高中高三(下)3月月考数学试卷(理科)(解析版) 题型:解答题
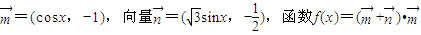 .
. ,且f(A)恰是f(x)在[0,
,且f(A)恰是f(x)在[0, ]上的最大值,求A,b和△ABC的面积.
]上的最大值,求A,b和△ABC的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com