
【题目】已知数列{an}的前n项和为Sn , 且满足4nSn=(n+1)2an(n∈N*).a1=1
(Ⅰ)求an;
(Ⅱ)设bn= ![]() ,数列{bn}的前n项和为Tn , 求证:Tn
,数列{bn}的前n项和为Tn , 求证:Tn ![]() .
.
【答案】(Ⅰ)解:∵4nSn=(n+1)2an(n∈N*),(1)
∴4(n﹣1)Sn﹣1=n2an﹣1 , (2)
由(1)(2),得:an=Sn﹣Sn﹣1= ![]() an﹣
an﹣ ![]() an﹣1(n≥2),
an﹣1(n≥2),
整理得: ![]() =
= ![]() =
= ![]() =1,
=1,
∴an=n3 .
(Ⅱ)证明:∵bn= ![]() ,a1=1,
,a1=1,
∴b1=1
当n≥2时,bn= ![]() <
< ![]() =
= ![]() ﹣
﹣ ![]() ,
,
∴数列{bn}的前n项和为Tn=b1+b2+…+bn<1+ ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]()
<1+ ![]() +(
+( ![]() ﹣
﹣ ![]() )+(
)+( ![]() ﹣
﹣ ![]() )+…+(
)+…+( ![]() ﹣
﹣ ![]() )=
)= ![]() ﹣
﹣ ![]() <
< ![]()
【解析】(Ⅰ)利用递推关系式可得an=Sn﹣Sn﹣1= ![]() an﹣
an﹣ ![]() an﹣1 , 整理得:
an﹣1 , 整理得: ![]() =
= ![]() =
= ![]() =1,于是可求an;(Ⅱ)由(Ⅰ)知an=n3 , 则bn=
=1,于是可求an;(Ⅱ)由(Ⅰ)知an=n3 , 则bn= ![]() =
= ![]() ,当n≥2时,利用放缩法得:bn=
,当n≥2时,利用放缩法得:bn= ![]() <
< ![]() =
= ![]() ﹣
﹣ ![]() ,从而可证:Tn<
,从而可证:Tn< ![]() .
.
【考点精析】认真审题,首先需要了解数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式).


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分8分)直线l过点P(4,1),
(1)若直线l过点Q(-1,6),求直线l的方程;
(2)若直线l在y轴上的截距是在x轴上的截距的2倍,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,其中[x]表示不超过x的最大整数.设n∈N* , 定义函数fn(x):f1(x)=f(x),f2(x)=f(f1(x)),…,fn(x)=f(fn﹣1(x))(n≥2),则下列说法正确的有 ①y=
,其中[x]表示不超过x的最大整数.设n∈N* , 定义函数fn(x):f1(x)=f(x),f2(x)=f(f1(x)),…,fn(x)=f(fn﹣1(x))(n≥2),则下列说法正确的有 ①y= ![]() 的定义域为
的定义域为 ![]() ;
;
②设A={0,1,2},B={x|f3(x)=x,x∈A},则A=B;
③ ![]() ;
;
④若集合M={x|f12(x)=x,x∈[0,2]},
则M中至少含有8个元素.( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,曲线Γ由曲线C1: ![]() (a>b>0,y≤0)和曲线C2:
(a>b>0,y≤0)和曲线C2: ![]() (a>0,b>0,y>0)组成,其中点F1 , F2为曲线C1所在圆锥曲线的焦点,点F3 , F4为曲线C2所在圆锥曲线的焦点,
(a>0,b>0,y>0)组成,其中点F1 , F2为曲线C1所在圆锥曲线的焦点,点F3 , F4为曲线C2所在圆锥曲线的焦点,
(Ⅰ)若F2(2,0),F3(﹣6,0),求曲线Γ的方程;
(Ⅱ)如图,作直线l平行于曲线C2的渐近线,交曲线C1于点A、B,求证:弦AB的中点M必在曲线C2的另一条渐近线上;
(Ⅲ)对于(Ⅰ)中的曲线Γ,若直线l1过点F4交曲线C1于点C、D,求△CDF1面积的最大值.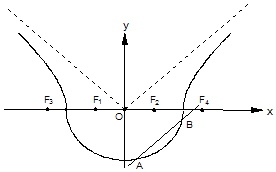
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是___________
![]() 用一个平面截一个球,得到的截面是一个圆;
用一个平面截一个球,得到的截面是一个圆;
![]() 圆台的任意两条母线延长后一定交于一点;
圆台的任意两条母线延长后一定交于一点;
![]() 有一个面为多边形,其余各面都是三角形的几何体叫做棱锥;
有一个面为多边形,其余各面都是三角形的几何体叫做棱锥;
![]() 若棱锥的侧棱长与底面多边形的边长相等,则该棱锥不可能是正六棱锥;
若棱锥的侧棱长与底面多边形的边长相等,则该棱锥不可能是正六棱锥;
![]() 用斜二测画法作出正三角形的直观图,则该直观图面积为原三角形面积的一半.
用斜二测画法作出正三角形的直观图,则该直观图面积为原三角形面积的一半.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的产品![]() 的直径均位于区间
的直径均位于区间![]() 内(单位:
内(单位: ![]() ).若生产一件产品
).若生产一件产品![]() 的直径位于区间
的直径位于区间![]() 内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品
内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品![]() 中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
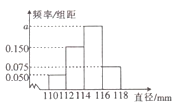
(1)求![]() 的值,并估计该厂生产一件
的值,并估计该厂生产一件![]() 产品的平均利润;
产品的平均利润;
(2)现用分层抽样法从直径位于区间![]() 内的产品中随机抽取一个容量为5的样本,从样本中随机抽取两件产品进行检测,求两件产品中至多有一件产品的直径位于区间
内的产品中随机抽取一个容量为5的样本,从样本中随机抽取两件产品进行检测,求两件产品中至多有一件产品的直径位于区间![]() 内的槪率.
内的槪率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m, n是两条不同的直线,![]() 是三个不同的平面, 给出下列四个命题:
是三个不同的平面, 给出下列四个命题:
①若m⊥α,n∥α,则m⊥n;; ②若α∥β, β∥r, m⊥α,则m⊥r;
③若m∥α,n∥α,则m∥n;; ④若α⊥r, β⊥r,则α∥β.
其中正确命题的序号是 ( )
A. ![]() ①和② B. ②和③ C. ③和④ D. ①和④
①和② B. ②和③ C. ③和④ D. ①和④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com