练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设f(x)＝x，若对于任意的实数t，恒有f(t＋|a|)＜f(t)，则实数a的取值范围是

    [　　]
    A．

    a＜－1，或a＞1

    B．

    －1＜a＜1，且a≠0

    C．

    0＜a＜1

    D．

    －1＜a＜1

    答案：B
    解析：


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：黑龙江省双鸭山市第一中学2011届高三上学期期中考试试题数学理综试题 题型：044

    已知函数f(x)＝lnx－ax＋－1(a∈R)

    (Ⅰ)当a≤时，讨论f(x)的单调性：

    (Ⅱ)设g(x)＝x2－2bx＋4，当a＝时，若对任意x1∈(0，2)，存在x2∈[1，2]，使f(x1)≥g(x2)，求实数b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：天津市新人教A版数学2012届高三单元测试37：变化率和导数计算 题型：044

    设函数f(x)＝ax3＋bx＋c是定义在R上的奇函数，且函数f(x)的图象在x＝1处的切线方程为y＝3x＋2．

    (Ⅰ)求a，b，c的值；

    (Ⅱ)若对任意x∈(0，1]都有f(x)≤成立，求实数k的取值范围；

    (Ⅲ)若对任意x∈(0，3]都有|f(x)－mx|≤16成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：新疆兵团二中2012届高三第六次月考数学文科试题 题型：044

    设函数f(x)＝x3＋3ax2＋bx＋c，g(x)＝x2－3x＋2，其中x∈R，a、b为常数，已知曲线y＝f(x)与y＝g(x)在点(2，0)处有相同的切线l．

    (Ⅰ)求a、b的值，并写出切线l的方程；

    (Ⅱ)若方程f(x)＋g(x)＝mx有三个互不相同的实根0、x1、x2，其中x1＜x2，且对任意的x∈[x1，x2]，f(x)＋g(x)＜m(x－1)恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年吉林省四校联合体高三第一次诊断性测试文科数学试卷（解析版） 题型：选择题

    设f(x)是定义在R上的偶函数，对x∈R，都有f(x+4)=f(x)，且当x∈[－2,0]时，f(x)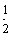＝()x－1，若在区间(－2，6]内关于x的方程f(x)－loga(x＋2)＝0(a＞1)恰有3个不同的实数根，则a的取值范围是

    A．(1,2)             B．(2，＋∞)         C．(1,)          D．(,2)

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年宁夏高三第一次模拟考试文科数学试卷 题型：选择题

    设f(x)是定义在R上的偶函数，对x∈R，都有f(x+4)=f(x)，且当x∈[－2,0]时，f(x)＝()x－1，若在区间(－2，6]内关于x的方程f(x)－loga(x＋2)＝0(a＞1)恰有3个不同的实数根，则a的取值范围是

    A．(1,2)        B. (2，＋∞)       C. (1,)       D. (,2)

     

    查看答案和解析>>

    同步练习册答案