
【题目】棉花的纤维长度是评价棉花质量的重要指标,某农科所的专家在土壤环境不同的甲、乙两块实验地分别种植某品种的棉花,为了评价该品种的棉花质量,在棉花成熟后,分别从甲、乙两地的棉花中各随机抽取20根棉花纤维进行统计,结果如下表:(记纤维长度不低于300mm的为“长纤维”,其余为“短纤维”)
纤维长度 | (0,100) | [100,200) | [200,300) | [300,400) | [400,500] |
甲地(根数) | 3 | 4 | 4 | 5 | 4 |
乙地(根数) | 1 | 1 | 2 | 10 | 6 |
(1)由以上统计数据,填写下面2×2列联表,并判断能否在犯错误概率不超过0.025的前提下认为“纤维长度与土壤环境有关系”.
甲地 | 乙地 | 总计 | |
长纤维 | |||
短纤维 | |||
总计 |
附:(1) ![]() ;(2)临界值表;
;(2)临界值表;
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)现从上述40根纤维中,按纤维长度是否为“长纤维”还是“短纤维”采用分层抽样的方法抽取8根进行检测,在这8根纤维中,记乙地“短纤维”的根数为X,求X的分布列及数学期望.
【答案】
(1)9;16;25;11;4;15;20;20;40
(2)由表可知在8根中乙地“短纤维”的根数为 ![]() ,X的可能取值为:0,1,2,3,
,X的可能取值为:0,1,2,3, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
∴X的分布列为:
X | 0 | 1 | 2 | 3 |
P | | | | |
∴ ![]()
【解析】解:(Ⅰ)根据已知数据得到如下2×2列联表:
甲地 | 乙地 | 总计 | |
长纤维 | 9 | 16 | 25 |
短纤维 | 11 | 4 | 15 |
总计 | 20 | 20 | 40 |
根据2×2列联表中的数据,可得 ![]()
所以,在犯错误概率不超过0.025的前提下认为“纤维长度与土壤环境有关系”.
【考点精析】掌握离散型随机变量及其分布列是解答本题的根本,需要知道在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


科目:高中数学 来源: 题型:
【题目】已知m>0, ![]() ,
, ![]() .
.
(1) 若p是q的充分不必要条件,求实数m的取值范围;
(2) 若m=5,“![]() ”为真命题,“
”为真命题,“![]() ”为假命题,求实数x的取值范围.
”为假命题,求实数x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:![]()
![]() 1
1![]() 证明直线l经过定点并求此点的坐标;
证明直线l经过定点并求此点的坐标;
![]() 2
2![]() 若直线l不经过第四象限,求k的取值范围;
若直线l不经过第四象限,求k的取值范围;
![]() 3
3![]() 若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设
若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设![]() 的面积为S,求S的最小值及此时直线l的方程.
的面积为S,求S的最小值及此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边长分别为a,b,c,且cos2B﹣cos2A=2sinC(sinA﹣sinC).
(1)求角B的大小;
(2)若 ![]() ,求2a+c的取值范围.
,求2a+c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax+a(a∈R),其中e为自然对数的底数.
(1)讨论函数y=f(x)的单调性;
(2)函数y=f(x)的图象与x轴交于A(x1 , 0),B(x2 , 0)两点,x1<x2 , 点C在函数y=f(x)的图象上,且△ABC为等腰直角三角形,记 ![]() ,求at﹣(a+t)的值.
,求at﹣(a+t)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面![]() 平面
平面![]() ,四边形
,四边形![]() 和
和![]() 是全等的等腰梯形,其中
是全等的等腰梯形,其中![]() ,且
,且![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 是
是![]() 的中点.
的中点.
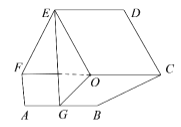
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)请在图中所给的点中找出两个点,使得这两点所在的直线与平面![]() 垂直,并给出证明;
垂直,并给出证明;
(Ⅲ)在线段![]() 上是否存在点,使得
上是否存在点,使得![]() 平面
平面![]() ?如果存在,求出
?如果存在,求出![]() 的长度;如果不存在,请说明理由.
的长度;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com