设函数f(x)=(x+2)2-2ln(x+2).
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若关于x的方程f(x)=x2+3x+a在区间[-1,1]上只有一个实数根,求实数a的取值范围.
解:(Ⅰ)函数f(x)的定义域为(-2,+∞),
因为f′(x)=2[(x+2)-
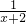
]=

,
所以 当-2<x<-1时,f′(x)<0;
当x>-1时,f′(x)>0.
故f(x)的单调递增区间是(-1,+∞);
f(x)的单调递减区间是(-2,-1)(注:-1处写成“闭的”亦可)
(Ⅱ)由f(x)=x
2+3x+a得:x-a+4-2ln(2+x)=0,
设g(x)=x-a+4-2ln(2+x),求导数得g′(x)=1-

=

在区间[-1,1]上加以讨论:
当-1<x<0时,g′(x)<0,而当0<x<1时,g′(x)>0,
故g(x)在[-1,0]上递减,在[0,1]上递增,
要使方程f(x)=x
2+3x+a在区间[-1,-1]上只有一个实数根,
则必须且只需g(0)=0,或
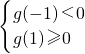
或

接下来分类:
①当g(0)=0时,解之得a=4-2ln2;
②当
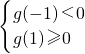
时,
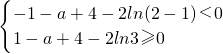
解之得a∈φ
③当

时,
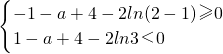
解之得a∈(5-2ln3,3]
综上所述,得a=4-2ln2,或a∈(5-2ln3,3]
所以实数a的取值范围(5-2ln3,3]∪{4-2ln2}.
分析:(Ⅰ)求出函数f(x)的导数f′(x),注意到函数的定义域为(-2,+∞),在此基础上讨论函数f′(x)的正负,可得函数的单调区间;
(Ⅱ)将函数f(x)的表达式代入,方程f(x)=x
2+3x+a变形为x-a+4-2ln(2+x)=0,然后令左边对应的函数为g(x),再通过求导数g′(x),得到在g(x)在[-1,0]上递减,在[0,1]上递增,问题转化为①函数的极小值等于0;②左边的最大值小于0,而右边的最大值大于或等于0;③左边的最大值大于或等于0,右边的最大值小于0.三种情况必据其一,因此分类讨论即可得出实数a的取值范围.
点评:本题考查了利用导数研究函数的单调性、利用导数研究函数的极值与最值,以及函数与方程之间的联系等知识点,是一道中档题.

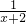 ]=
]= ,
, =
=
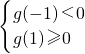 或
或
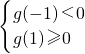 时,
时,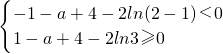
 时,
时,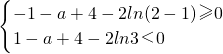


 轻松暑假总复习系列答案
轻松暑假总复习系列答案 的最小值;
的最小值; 的最小值;
的最小值;