
设数列{an}的前n项和为Sn.已知a1=1,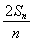 =an+1-
=an+1-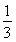 n2-n-
n2-n-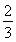 ,n∈N*.
,n∈N*.
(1)求a2的值;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有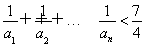 .
.
(1)a2=4.(2)an=n2(n≥2),(3)见解析
【解析】(1)【解析】
∵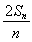 =an+1-
=an+1-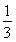 n2-n-
n2-n-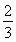 ,n∈N*.
,n∈N*.
∴当n=1时,2a1=2S1=a2-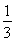 -1-
-1-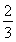 =a2-2.
=a2-2.
又a1=1,∴a2=4.
(2)【解析】
∵ =an+1-
=an+1-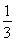 n2-n-
n2-n-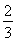 ,n∈N*.
,n∈N*.
∴2Sn=nan+1-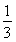 n3-n2-
n3-n2-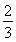 n=nan+1-
n=nan+1-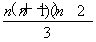 ,①
,①
∴当n≥2时,2Sn-1=(n-1)an-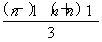 ,②
,②
由①-②,得2Sn-2Sn-1=nan+1-(n-1)an-n(n+1).
∵2an=2Sn-2Sn-1,
∴2an=nan+1-(n-1)an-n(n+1),∴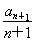 -
-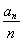 =1.
=1.
∴数列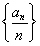 是以首项为
是以首项为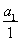 =1,公差为1的等差数列.
=1,公差为1的等差数列.
∴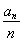 =1+1×(n-1)=n,∴an=n2(n≥2),
=1+1×(n-1)=n,∴an=n2(n≥2),
当n=1时,上式显然成立.∴an=n2,n∈N*.
(3)证明:由(2)知,an=n2,n∈N*,
①当n=1时,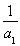 =1<
=1<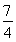 ,∴原不等式成立.
,∴原不等式成立.
②当n=2时,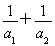 =1+
=1+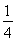 <
<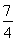 ,∴原不等式亦成立.
,∴原不等式亦成立.
③当n≥3时,∵n2>(n-1)·(n+1),∴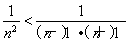 ,
,
∴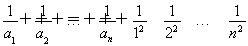
<1+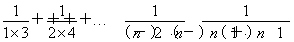
=1+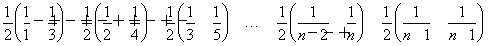
=1+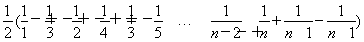
=1+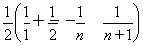 =
=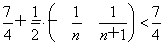 ,
,
∴当n≥3时,原不等式亦成立.
综上,对一切正整数n,有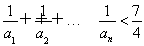 .
.


科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第三章第4课时练习卷(解析版) 题型:解答题
已知cosα=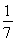 ,cos(α-β)=
,cos(α-β)=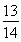 ,且0<β<α<
,且0<β<α<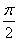 ,求β.
,求β.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第三章第1课时练习卷(解析版) 题型:解答题
已知一扇形的中心角是α,所在圆的半径是R.
(1)若α=60°,R=10cm,求扇形的弧长及该弧所在的弓形面积;
(2)若扇形的周长是一定值C(C>0),当α为多少弧度时,该扇形有最大面积?
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第三章第1课时练习卷(解析版) 题型:填空题
若角θ同时满足sinθ<0且tanθ<0,则角θ的终边一定落在第________象限.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第七章第3课时练习卷(解析版) 题型:解答题
已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=145.
(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga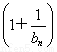 (其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与
(其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与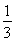 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第七章第2课时练习卷(解析版) 题型:解答题
ABCD为直角梯形,∠BCD=∠CDA=90°,AD=2BC=2CD,P为平面ABCD外一点,且PB⊥BD.
(1)求证:PA⊥BD;
(2)若PC与CD不垂直,求证:PA≠PD.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第七章第1课时练习卷(解析版) 题型:填空题
观察下列各式:a+b=1;a2+b2=3;a3+b3=4;a4+b4=7;a5+b5=11;…;则a10+b10=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第一章第1课时练习卷(解析版) 题型:填空题
设P、Q为两个非空实数集合,定义集合P+Q={a+b|a∈P,b∈Q},若P={0,2,5},Q={1,2,6},则P+Q中元素的个数为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com