
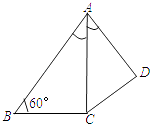
【题目】如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC= ![]() ,求AB的长.
,求AB的长. 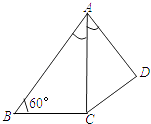
【答案】解:在△ADC中,已知AC=6,AD=5,S△ADC= ![]() ,
,
则由S△ADC= ![]() ACADsin∠DAC,
ACADsin∠DAC,
∴sin∠DAC= ![]() ,又∠DAC为三角形的内角,
,又∠DAC为三角形的内角,
∴∠DAC=30°或150°,
若∠DAC=150°,又AC为∠DAB的平分线,
得∠BAC=∠DAC=150°,又∠ABC=60°,
∴∠BAC+∠ABC=210°,矛盾,
∴∠DAC=150°不合题意,舍去,
∴∠BAC=∠DAC=30°,又∠ABC=60°,
∴∠ACB=90°,又AC=6,
∴由正弦定理 ![]() =
= ![]() 得:AB=
得:AB= ![]() =2
=2 ![]() .
.
【解析】利用三角形的面积公式表示出三角形ADC的面积,把AC,AD的值代入,求出sin∠DAC的值,由∠DAC为三角形的内角,利用特殊角的三角函数值求出∠DAC的度数,根据AC为角平分线,得到∠DAC=∠BAC,可得出∠BAC的度数,由∠ABC的度数,利用三角形的内角和定理求出∠ACB的度数,由AC,sin∠ABC,以及sin∠ACB的值,利用正弦定理即可求出AB的长.
【考点精析】本题主要考查了正弦定理的定义的相关知识点,需要掌握正弦定理:![]() 才能正确解答此题.
才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某中学刚搬迁到新校区,学校考虑,若非住校生上学路上单程所需时间人均超过20分钟,则学校推迟5分钟上课.为此,校方随机抽取100个非住校生,调查其上学路上单程所需时间(单位:分钟),根据所得数据绘制成如下频率分布直方图,其中时间分组为[0,10),[10,20),[20,30),[30,40),[40,50]. 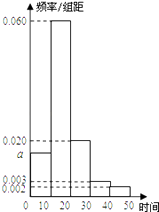
(1)求频率分布直方图中a的值;
(2)从统计学的角度说明学校是否需要推迟5分钟上课;
(3)若从样本单程时间不小于30分钟的学生中,随机抽取2人,求恰有一个学生的单程时间落在[40,50]上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若钝角三角形的三边长和面积都是整数,则称这样的三角形为“钝角整数三角形”,下列选项中能构成一个“钝角整数三角形”三边长的是( )
A.2,3,4
B.2,4,5
C.5,5,6
D.4,13,15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)曲线![]() 与
与![]() 相交于
相交于![]() 两点,求过
两点,求过![]() 两点且面积最小的圆的标准方程.
两点且面积最小的圆的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有大型超市200家、中型超市400家、小型超市1400 家.为掌握各类超市的营业情况,现按分层抽样方法抽取一个容量为100的样本,应抽取中型超市( )
A.70家
B.50家
C.20家
D.10家
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,对于集合
,对于集合![]() 的两个非空子集
的两个非空子集![]() ,
, ![]() ,若
,若![]() ,则称
,则称![]() 为集合
为集合![]() 的一组“互斥子集”.记集合
的一组“互斥子集”.记集合![]() 的所有“互斥子集”的组数为
的所有“互斥子集”的组数为![]() (视
(视![]() 与
与![]() 为同一组“互斥子集”).
为同一组“互斥子集”).
(1)写出![]() ,
, ![]() ,
, ![]() 的值;
的值;
(2)求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图,估计这次测试中数学成绩的平均分、众数、中位数分别是( ) 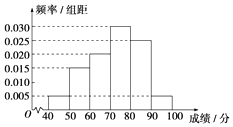
A.73.3,75,72
B.72,75,73.3
C.75,72,73.3
D.75,73.3,72
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com