
【题目】已知数列{an}满足a1= ![]() 且an+1=
且an+1= ![]() .设bn+2=3
.设bn+2=3 ![]() ,数列{cn}满足cn=anbn .
,数列{cn}满足cn=anbn .
(1)求数列{bn}通项公式;
(2)求数列{cn}的前n项和Sn;
(3)若cn≤ ![]() +m﹣1对一切正整数n恒成立,求实数m的取值范围.
+m﹣1对一切正整数n恒成立,求实数m的取值范围.
【答案】
(1)解:由 ![]() 得,数列{an}是公比为
得,数列{an}是公比为 ![]() 的等比数列,
的等比数列,
则 ![]() ,
,
所以 ![]() ,即bn=3n+1
,即bn=3n+1
(2)解:由(1)知, ![]() ,bn=3n+1,
,bn=3n+1,
则 ![]() .
.
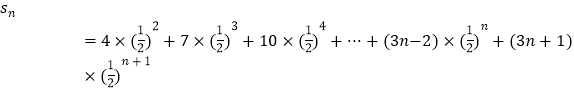 ,①
,①
则 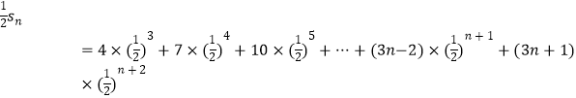 ,②
,②
①﹣②两式相减得 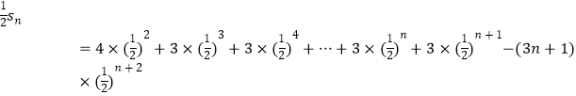
= ![]()
= 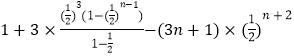
= ![]() .
.
所以 ![]()
(3)解:因为 ![]() ,
,
所以 ![]() =
= ![]() ,
,
则数列{cn}单调递减,
∴当n=1时,cn取最大值是 ![]() ,
,
又∵cn≤ ![]() +m﹣1对一切正整数n恒成立,
+m﹣1对一切正整数n恒成立,
∴ ![]() +m﹣1≥
+m﹣1≥ ![]() ,即m2+4m﹣5≥0,
,即m2+4m﹣5≥0,
解得:m≥1或m≤﹣5
【解析】(1)利用等比数列的通项公式计算可知{an}的通项,进而代入计算即得结论;(2)通过可知数列{cn}的通项公式,进而利用错位相减法计算即得结论;(3)通过分析可知数列{cn}的单调性,进而转化为解不等式问题,计算即得结论.
【考点精析】关于本题考查的数列的前n项和和数列的通项公式,需要了解数列{an}的前n项和sn与通项an的关系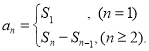 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】把函数y=sin3x的图象向右平移 ![]() 个长度单位,所得曲线的对应函数式( )
个长度单位,所得曲线的对应函数式( )
A.y=sin(3x﹣ ![]() )
)
B.y=sin(3x+ ![]() )
)
C.y=sin(3x﹣ ![]() )
)
D.y=sin(3x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 且a3=7,a5+a7=26
(1)求an及Sn;
(2)令bn= ![]() (n∈N*)求数列{bn}的前n项和Tn .
(n∈N*)求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 的最大值为6,求常数
的最大值为6,求常数![]() 的值;
的值;
(2)若函数![]() 有两个零点
有两个零点![]() 和
和![]() ,求
,求![]() 的取值范围,并求
的取值范围,并求![]() 和
和![]() 的值;
的值;
(3)在(1)的条件下,若![]() ,讨论函数
,讨论函数![]() 的零点个数.
的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() (x∈R)且x≠﹣1,g(x)=x2+2(x∈R).
(x∈R)且x≠﹣1,g(x)=x2+2(x∈R).
(1)求f(2),g(2)的值;
(2)求f[g(2)]的值;
(3)求f[g(x)]和g[f(x)]的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面α与平面β相交于直线l,l1在平面α内,l2在平面β内,若直线l1和l2是异面直线,则下列说法正确的是( )
A.l与都相交l1 , l2
B.l至少与l1 , l2中的一条相交
C.l至多与l1 , l2中的一条相交
D.l与l1 , l2都不相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=x+ ![]() (a>0)在区间
(a>0)在区间 ![]() 上单调递减,在区间
上单调递减,在区间 ![]() 上单调递增;函数
上单调递增;函数 ![]()
(1)请写出函数f(x)=x2+ ![]() (a>0)与函数g(x)=xn+
(a>0)与函数g(x)=xn+ ![]() (a>0,n∈N,n≥3)在(0,+∞)的单调区间(只写结论,不证明);
(a>0,n∈N,n≥3)在(0,+∞)的单调区间(只写结论,不证明);
(2)求函数h(x)的最值;
(3)讨论方程h2(x)﹣3mh(x)+2m2=0(0<m≤30)实根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
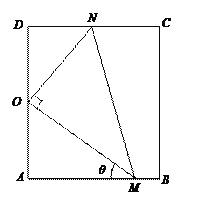
【题目】如图,矩形ABCD是某小区户外活动空地的平面示意图,其中AB=50![]() 米,AD=100米,现拟在直角三角形OMN内栽植草坪供儿童踢球娱乐(其中,点O为AD的中点,OM⊥ON,点M在AB上,点N在CD上),将破旧的道路AM重新铺设.已知草坪成本为每平方米20元,新道路AM成本为每米500元,设∠OMA=θ,记草坪栽植与新道路铺设所需的总费用为f(θ).
米,AD=100米,现拟在直角三角形OMN内栽植草坪供儿童踢球娱乐(其中,点O为AD的中点,OM⊥ON,点M在AB上,点N在CD上),将破旧的道路AM重新铺设.已知草坪成本为每平方米20元,新道路AM成本为每米500元,设∠OMA=θ,记草坪栽植与新道路铺设所需的总费用为f(θ).
(1)求f(θ)关于θ函数关系式,并写出定义域;
(2)为节约投入成本,当tanθ为何值时,总费用 f(θ)最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com