
【题目】如图,在三棱锥![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,
的中点, ![]() 在
在![]() 上,且
上,且![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)在线段上![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角
![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

【答案】(1)见解析; (2)见解析.
【解析】试题分析:第(1)问证明![]() 平面
平面![]() ,基本思路是证明
,基本思路是证明![]() 平面
平面![]() 内的两条相交直线垂直,注意合理利用题设条件给出的数量关系和图形关系;第(2)问应抓住两点找到问题的求解方向:一是点
内的两条相交直线垂直,注意合理利用题设条件给出的数量关系和图形关系;第(2)问应抓住两点找到问题的求解方向:一是点![]() 的预设位置,二是二面角
的预设位置,二是二面角![]() 的位置.涉及空间二面角的问题,可以从两个不同的方法上得到求解,即常规法和向量法
的位置.涉及空间二面角的问题,可以从两个不同的方法上得到求解,即常规法和向量法
试题解析:
(1)由![]() ,
, ![]() ,
,
![]() 是
是![]() 的中点,得
的中点,得![]() .
.
因为![]() 底面
底面![]() ,所以
,所以![]() .
.
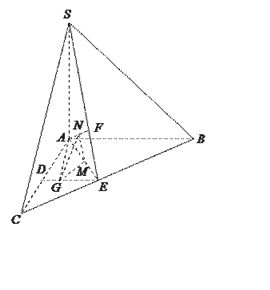 在
在![]() 中,
中, ![]() ,所以
,所以![]() .
.
因此![]() ,又因为
,又因为![]() ,
,
所以![]() ,
,
则![]() ,即
,即![]() . 因为
. 因为![]() 底面
底面![]() ,所以
,所以![]() ,又
,又![]() ,
,
所以![]() 底面
底面![]() ,则
,则![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)方法一:假设满足条件的点![]() 存在,并设
存在,并设![]() .
.
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
又由![]() ,
, ![]() ,得
,得![]() 平
平
面![]() .
.
作![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,则
,则![]() .
.
于是![]() 为二面角
为二面角![]() 的平面角,
的平面角,
即![]() ,由此可得
,由此可得![]() .
.
由![]() ,得
,得![]() ,于是有
,于是有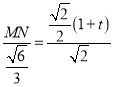 ,
, ![]() .
.
在![]() 中,
中, ![]() ,即
,即![]() ,解得
,解得![]() .
.
于是满足条件的点![]() 存在,且
存在,且![]() .
.
(2)方法二:假设满足条件的点![]() 存在,并设
存在,并设![]() .以
.以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
, ![]() ,
, ![]() 为
为![]() ,
, ![]() ,
, ![]() 轴建立空间直线坐标系
轴建立空间直线坐标系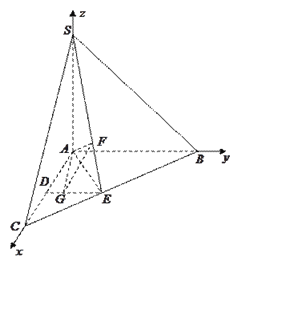
![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
,
![]() .由
.由![]() 得
得![]() .
.
所以![]() ,
, ![]() ,
, ![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则
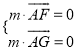 ,即
,即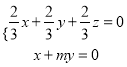 ,取
,取![]() ,得
,得![]() ,
, ![]() ,即
,即![]() .设平面
.设平面![]() 的法向量为
的法向量为![]() ,则
,则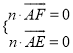 ,即
,即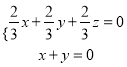 ,取
,取![]() ,得
,得![]() ,
, ![]() ,即
,即![]() .由二面角
.由二面角![]() 的大小为
的大小为![]() ,得
,得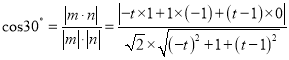 ,化简得
,化简得![]() ,又
,又![]() ,求得
,求得![]() . 于是满足条件的点
. 于是满足条件的点![]() 存在,且
存在,且![]() .
.
点晴:本题考查的是线面垂直的证明和二面角的求解.第(1)问证明![]() 平面
平面![]() ,基本思路是证明
,基本思路是证明![]() 平面
平面![]() 内的两条相交直线垂直,注意合理利用题设条件给出的数量关系和图形关系;第(2)问应抓住两点找到问题的求解方向:一是点
内的两条相交直线垂直,注意合理利用题设条件给出的数量关系和图形关系;第(2)问应抓住两点找到问题的求解方向:一是点![]() 的预设位置,二是二面角
的预设位置,二是二面角![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】
为庆祝“2017年中国长春国际马拉松赛”,某单位在庆祝晚会中进行嘉宾现场抽奖活动.抽奖盒中装有大小相同的6个小球,分别印有“长春马拉松”和“美丽长春”两种标志,摇匀后,规定参加者每次从盒中同时抽取两个小球(登记后放回并摇匀),若抽到的两个小球都印有“长春马拉松”即可中奖,并停止抽奖,否则继续,但每位嘉宾最多抽取3次.已知从盒中抽取两个小球不都是“美丽长春”标志的概率为![]() .
.
(Ⅰ)求盒中印有“长春马拉松”标志的小球个数;
(Ⅱ)用η表示某位嘉宾抽奖的次数,求η的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对应的边分别为a,b,c,sinC+sin(A﹣B)=3sin2B.若 ![]() ,则
,则 ![]() =( )
=( )
A.![]()
B.3
C.![]() 或3
或3
D.3或 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:若0<a<1,则不等式ax2﹣2ax+1>0在R上恒成立,命题q:a≥1是函数 ![]() 在(0,+∞)上单调递增的充要条件;在命题 ①“p且q”、②“p或q”、③“非p”、④“非q”中,假命题是 .
在(0,+∞)上单调递增的充要条件;在命题 ①“p且q”、②“p或q”、③“非p”、④“非q”中,假命题是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知顶点在原点,焦点在x轴上的抛物线被直线y=2x+1截得的弦长为 ![]() .
.
(1)求抛物线的方程;
(2)若抛物线与直线y=2x﹣5无公共点,试在抛物线上求一点,使这点到直线y=2x﹣5的距离最短.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 ![]() 的最小正周期为π,若其图象向左平移
的最小正周期为π,若其图象向左平移 ![]() 个单位后得到的函数为奇函数,则函数f(x)的图象( )
个单位后得到的函数为奇函数,则函数f(x)的图象( )
A.关于点 ![]() 对称
对称
B.关于点 ![]() 对称
对称
C.关于直线 ![]() 对称
对称
D.关于直线 ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2017年第一季度五省![]() 情况图,则下列陈述正确的是( )
情况图,则下列陈述正确的是( )

①2017年第一季度 ![]() 总量和增速均居同一位的省只有1个;
总量和增速均居同一位的省只有1个;
②与去年同期相比,2017年第一季度五个省的![]() 总量均实现了增长;
总量均实现了增长;
③去年同期的![]() 总量前三位是江苏、山东、浙江;
总量前三位是江苏、山东、浙江;
④2016年同期浙江的![]() 总量也是第三位.
总量也是第三位.
A. ①② B. ②③④ C. ②④ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com