
【题目】
为庆祝“2017年中国长春国际马拉松赛”,某单位在庆祝晚会中进行嘉宾现场抽奖活动.抽奖盒中装有大小相同的6个小球,分别印有“长春马拉松”和“美丽长春”两种标志,摇匀后,规定参加者每次从盒中同时抽取两个小球(登记后放回并摇匀),若抽到的两个小球都印有“长春马拉松”即可中奖,并停止抽奖,否则继续,但每位嘉宾最多抽取3次.已知从盒中抽取两个小球不都是“美丽长春”标志的概率为![]() .
.
(Ⅰ)求盒中印有“长春马拉松”标志的小球个数;
(Ⅱ)用η表示某位嘉宾抽奖的次数,求η的分布列和期望.
【答案】(Ⅰ)3;(Ⅱ)分布列见解析,期望为![]() .
.
【解析】试题分析:
(1)利用题意结合对立事件公式可得![]() ;
;
(2)利用题意可得![]() 的取值为
的取值为![]() ,写出分布列,结合分布列可得期望为
,写出分布列,结合分布列可得期望为![]() .
.
试题解析:
(Ⅰ)设印有“美丽长春”的球有n个,同时抽两球不都是“美丽长春”标志为事件A,则同时抽取两球都是“美丽长春”标志的概率是P(![]() )=
)=![]() ,
,
由对立事件的概率:P(A)=1-P(![]() )=
)=![]() .
.
即P(![]() )=
)=![]() =
=![]() ,解得n=3.
,解得n=3.
(Ⅱ)由已知,两种球各三个,η可能取值分别为1,2,3,
P(η=1)=![]() =
=![]() ,
,
P(η=2)=![]() ·
·![]() +
+![]() ·
·![]() =
=![]() ,
,
P(η=3)=1-P(η=1)-P(η=2)=![]() .
. ![]()
![]()
则η的分布列为
η | 1 | 2 | 3 |
P |
|
|
|
所以E(η)=1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 的定义域为集合A,函数g(x)=lg(﹣x2+2x+m)的定义域为集合B.
的定义域为集合A,函数g(x)=lg(﹣x2+2x+m)的定义域为集合B.
(1)当m=3时,求A∩(RB)
(2)若A∩B={x|﹣1<x<4},求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() cosx(sinx+cosx).
cosx(sinx+cosx).
(1)若0<α< ![]() ,且sinα=
,且sinα= ![]() ,求f(α)的值;
,求f(α)的值;
(2)求函数f(x)的最小正周期及单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若x,y∈[﹣1,1],x+y≠0有(x+y)[f(x)+f(y)]>0.
(1)判断f(x)的单调性,并加以证明;
(2)解不等式 ![]() ;
;
(3)若f(x)≤m2﹣2am+1对所有x∈[﹣1,1],a∈[﹣1,1]恒成立.求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,抛物线C1:x2=4y,C2:x2=-2py(p>0).点M(x0,y0)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O).当x0=1-![]() 时,切线MA的斜率为-
时,切线MA的斜率为-![]() .
.
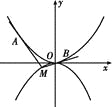
(1)求p的值;
(2)当M在C2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在![]() 内的产品为合格品,否则为不合格品,统计结果如表:
内的产品为合格品,否则为不合格品,统计结果如表:
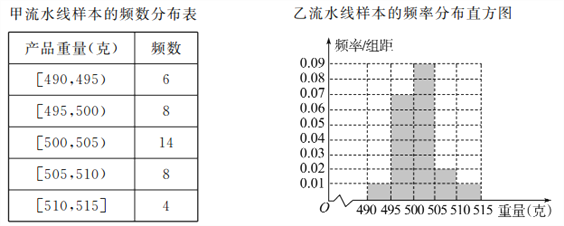
(Ⅰ)求甲流水线样本合格的频率;
(Ⅱ)从乙流水线上重量值落在![]() 内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率.
内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,
的中点, ![]() 在
在![]() 上,且
上,且![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)在线段上![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角
![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com