
【题目】设函数![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)如果对任意![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ),![]() 时,函数
时,函数![]() 在
在![]() 内单调递减;当
内单调递减;当![]() 时,函数
时,函数![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 内单调递增.(Ⅱ)
内单调递增.(Ⅱ)![]() .
.
【解析】试题分析:
(1)结合导函数的解析式讨论可得,![]() 时,函数
时,函数![]() 在
在![]() 内单调递减;当
内单调递减;当![]() 时,函数
时,函数![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 内单调递增.
内单调递增.
(2)构造新函数令![]() ,结合
,结合![]() 的性质可得实数
的性质可得实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(Ⅰ)![]() .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 内单调递减;
内单调递减;
当![]() 时,令
时,令![]() ,有
,有![]() ,此时当
,此时当![]() 时,
时,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() 单调递增.
单调递增.
综上所述,![]() 时,函数
时,函数![]() 在
在![]() 内单调递减;当
内单调递减;当![]() 时,函数
时,函数![]() 在
在
![]() 内单调递减,在
内单调递减,在![]() 内单调递增.
内单调递增.
(Ⅱ)令![]() ,即
,即![]() .
.
令![]() ,则
,则![]()
![]() ,则
,则![]() 在
在![]() 内单调递增,所以
内单调递增,所以![]() ,故
,故![]() .
.
当![]() 时,
时,![]() 故当
故当![]() 在区间
在区间![]() 内恒成立时,必有
内恒成立时,必有![]() .
.
当![]() 时,
时,![]() ,由(Ⅰ)知函数
,由(Ⅰ)知函数![]() 在
在![]() 上单调递减,即
上单调递减,即![]() 时,
时,
![]() 不符合题意,舍去.
不符合题意,舍去.
当![]() 时,令
时,令![]() ,则
,则
![]() ,
,
所以![]() 在
在![]() 时单调递增,所以
时单调递增,所以![]() 恒成立,即
恒成立,即![]() 恒成立,满足题意.
恒成立,满足题意.
综上,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣2ax+b(a>0)在区间[﹣1,4]上有最大值10和最小值1.设g(x)= ![]() .
.
(1)求a、b的值;
(2)证明:函数g(x)在[ ![]() ,+∞)上是增函数;
,+∞)上是增函数;
(3)若不等式g(2x)﹣k2x≥0在x∈[﹣1,1]上有解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)的定义域是[0,2],则函数g(x)= ![]() 的定义域是( )
的定义域是( )
A.[0,1)∪(1,2]
B.[0,1)∪(1,4]
C.[0,1)
D.(1,4]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知圆C:x2+y2=4和直线l:x=4,M为l上一动点,A1 , A2为圆C与x轴的两个交点,直线MA1 , MA2与圆C的另一个交点分别为P、Q.
(1)若M点的坐标为(4,2),求直线PQ方程;
(2)求证直线PQ过定点,并求出此定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究一片大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:cm),根据所得数据画出的样本频率分布直方图如图,那么在这片树木中底部周长大于100cm的株树大约中( ) 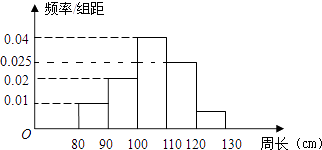
A.3000
B.6000
C.7000
D.8000
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=log4(4x+1)+ax(a∈R).
(1)若函数f(x)是定义在R上的偶函数,求a的值;
(2)若不等式f(x)+f(﹣x)≥mt+m对任意x∈R,t∈[﹣2,1]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,左、右顶点分别为
,左、右顶点分别为![]() 为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为
为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为![]() .设点
.设点![]() ,连接PA交椭圆于点C,坐标原点为O.
,连接PA交椭圆于点C,坐标原点为O.
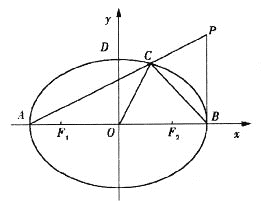
(I)求椭圆E的方程;
(II)若三角形ABC的面积不大于四边形OBPC的面积,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
为庆祝“2017年中国长春国际马拉松赛”,某单位在庆祝晚会中进行嘉宾现场抽奖活动.抽奖盒中装有大小相同的6个小球,分别印有“长春马拉松”和“美丽长春”两种标志,摇匀后,规定参加者每次从盒中同时抽取两个小球(登记后放回并摇匀),若抽到的两个小球都印有“长春马拉松”即可中奖,并停止抽奖,否则继续,但每位嘉宾最多抽取3次.已知从盒中抽取两个小球不都是“美丽长春”标志的概率为![]() .
.
(Ⅰ)求盒中印有“长春马拉松”标志的小球个数;
(Ⅱ)用η表示某位嘉宾抽奖的次数,求η的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com