
【题目】已知函数f(x)= ![]() cosx(sinx+cosx).
cosx(sinx+cosx).
(1)若0<α< ![]() ,且sinα=
,且sinα= ![]() ,求f(α)的值;
,求f(α)的值;
(2)求函数f(x)的最小正周期及单调递增区间.
【答案】
(1)解:∵0<α< ![]() ,且sinα=
,且sinα= ![]() ,
,
∴cosα= ![]() ,
,
∴f(α)= ![]() cosα(sinα+cosα)
cosα(sinα+cosα)
= ![]() ×
× ![]() ×(
×( ![]() +
+ ![]() )
)
= ![]() ;
;
(2)解:函数f(x)= ![]() cosx(sinx+cosx)
cosx(sinx+cosx)
= ![]() (cosxsinx+cos2x)
(cosxsinx+cos2x)
= ![]() sin2x+
sin2x+ ![]() cos2x+
cos2x+ ![]()
=sin(2x+ ![]() )+
)+ ![]() ,
,
∴f(x)的最小正周期为π;
令﹣ ![]() +2kπ≤2x+
+2kπ≤2x+ ![]() ≤
≤ ![]() +2kπ,k∈Z,
+2kπ,k∈Z,
解得﹣ ![]() +kπ≤x≤
+kπ≤x≤ ![]() +kπ,k∈Z,
+kπ,k∈Z,
∴函数f(x)的单调减区间为[﹣ ![]() +kπ,
+kπ, ![]() +kπ],k∈Z
+kπ],k∈Z
【解析】(1)根据同角的三角函数关系,求出sinα、cosα的值,再计算f(α)的值;(2)化函数f(x)为正弦型函数,即可求出f(x)的最小正周期和单调减区间.


科目:高中数学 来源: 题型:
【题目】若函数y=f(x)的定义域是[0,2],则函数g(x)= ![]() 的定义域是( )
的定义域是( )
A.[0,1)∪(1,2]
B.[0,1)∪(1,4]
C.[0,1)
D.(1,4]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,左、右顶点分别为
,左、右顶点分别为![]() 为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为
为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为![]() .设点
.设点![]() ,连接PA交椭圆于点C,坐标原点为O.
,连接PA交椭圆于点C,坐标原点为O.
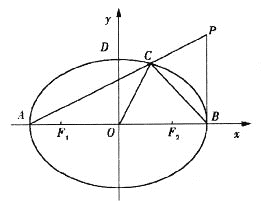
(I)求椭圆E的方程;
(II)若三角形ABC的面积不大于四边形OBPC的面积,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2ax+5(a>1).
(1)若函数f(x)的定义域和值域均为[1,a],求实数a的值;
(2)若f(x)在区间(﹣∞,2],上是减函数,且对任意的x1 , x2∈[1,a+1],总有|f(x1)﹣f(x2)|≤4,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
为庆祝“2017年中国长春国际马拉松赛”,某单位在庆祝晚会中进行嘉宾现场抽奖活动.抽奖盒中装有大小相同的6个小球,分别印有“长春马拉松”和“美丽长春”两种标志,摇匀后,规定参加者每次从盒中同时抽取两个小球(登记后放回并摇匀),若抽到的两个小球都印有“长春马拉松”即可中奖,并停止抽奖,否则继续,但每位嘉宾最多抽取3次.已知从盒中抽取两个小球不都是“美丽长春”标志的概率为![]() .
.
(Ⅰ)求盒中印有“长春马拉松”标志的小球个数;
(Ⅱ)用η表示某位嘉宾抽奖的次数,求η的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】王府井百货分店今年春节期间,消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该分店经理对春节前7天参加抽奖活动的人数进行统计, ![]() 表示第
表示第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 5 | 8 | 8 | 10 | 14 | 15 | 17 |
经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)判断变量![]() 与
与![]() 之间是正相关还是负相关;
之间是正相关还是负相关;
(3)若该活动只持续10天,估计共有多少名顾客参加抽奖.
参与公式:  ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:若0<a<1,则不等式ax2﹣2ax+1>0在R上恒成立,命题q:a≥1是函数 ![]() 在(0,+∞)上单调递增的充要条件;在命题 ①“p且q”、②“p或q”、③“非p”、④“非q”中,假命题是 .
在(0,+∞)上单调递增的充要条件;在命题 ①“p且q”、②“p或q”、③“非p”、④“非q”中,假命题是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com