
【题目】设函数![]() 是偶函数
是偶函数![]() 的导函数,
的导函数,![]() 在区间
在区间![]() 上的唯一零点为2,并且当
上的唯一零点为2,并且当![]() 时,
时,![]() ,则使得
,则使得![]() 成立的
成立的![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】令g(x)=xf(x),g′(x)=xf′(x)+f(x),
当x∈(﹣1,1)时,xf′(x)+f(x)<0,
∴g(x)在(﹣1,1)递减,
而g(﹣x)=﹣xf(﹣x)=﹣xf(x)=﹣g(x),
∴g(x)在R是奇函数,
∵f(x)在区间(0,+∞)上的唯一零点为2,
即g(x)在区间(0,+∞)上的唯一零点为2,
∴g(x)在(﹣∞,﹣1)递增,在(﹣1,1)递减,在(1,+∞)递增,
g(0)=0,g(2)=0,g(﹣2)=0,
如图示:,
x≥0时,f(x)<0,即xf(x)<0,由图象得:0≤x<2,
x<0时,f(x)<0,即xf(x)>0,由图象得:﹣2<x<0,
综上:x∈(﹣2,2),
故选:A.


科目:高中数学 来源: 题型:
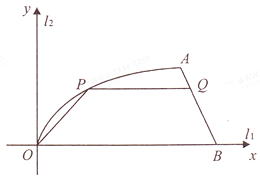
【题目】如图,某小区内有两条互相垂直的道路![]() 与
与![]() ,平面直角坐标系
,平面直角坐标系![]() 的第一象限有一块空地
的第一象限有一块空地![]() ,其边界
,其边界![]() 是函数
是函数![]() 的图象,前一段曲线
的图象,前一段曲线![]() 是函数
是函数![]() 图象的一部分,后一段
图象的一部分,后一段![]() 是一条线段.测得
是一条线段.测得![]() 到
到![]() 的距离为8米,到
的距离为8米,到![]() 的距离为16米,
的距离为16米,![]() 长为20米.
长为20米.
(1)求函数![]() 的解析式;
的解析式;
(2)现要在此地建一个社区活动中心,平面图为梯形![]() (其中
(其中![]() ,
,![]() 为两底边),问:梯形的高为多少米时,该社区活动中心的占地面积最大,并求出最大面积.
为两底边),问:梯形的高为多少米时,该社区活动中心的占地面积最大,并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于直线l:ax+by+c=0和点P1(x1 , y1),P2(x2 , y2),记η=(ax1+by1+c)(ax2+by2+c),若η<0,则称点P1 , P2被直线l分隔,若曲线C与直线l没有公共点,且曲线C上存在点P1、P2被直线l分隔,则称直线l为曲线C的一条分隔线.
(1)求证:点A(1,2),B(﹣1,0)被直线x+y﹣1=0分隔;
(2)若直线y=kx是曲线x2﹣4y2=1的分隔线,求实数k的取值范围;
(3)动点M到点Q(0,2)的距离与到y轴的距离之积为1,设点M的轨迹为曲线E,求证:通过原点的直线中,有且仅有一条直线是E的分隔线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】狄利克雷函数是高等数学中的一个典型函数,若![]() ,则称
,则称![]() 为狄利克雷函数.对于狄利克雷函数
为狄利克雷函数.对于狄利克雷函数![]() ,给出下面4个命题:①对任意
,给出下面4个命题:①对任意![]() ,都有
,都有![]() ;②对任意
;②对任意![]() ,都有
,都有![]() ;③对任意
;③对任意![]() ,都有
,都有![]() ,
, ![]() ;④对任意
;④对任意![]() ,都有
,都有![]() .其中所有真命题的序号是( )
.其中所有真命题的序号是( )
A. ①④ B. ②③ C. ①②③ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区![]() 年至
年至![]() 年农村居民家庭纯收入
年农村居民家庭纯收入![]() (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入 | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析![]() 年至
年至![]() 年该地区农村居民家庭人均纯收入的变化情况,并预测该地区
年该地区农村居民家庭人均纯收入的变化情况,并预测该地区![]() 年农村居民家庭人均纯收入.
年农村居民家庭人均纯收入.
![]() 注:
注: ,
,![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从学生会宣传部6名成员(其中男生4人,女生2人)中,任选3人参加某省举办的“我看中国改革开放三十年”演讲比赛活动.
(1)设所选3人中女生人数为ξ,求ξ的分布列;
(2)求男生甲或女生乙被选中的概率;
(3)设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P(B)和P(B|A).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的奇函数f(x)且满足f(1+x)=-f(3-x),且f(1)≠0,若函数g(x)=x6+f(1)cos4x-3有且只有唯一的零点,则f(2018)+f(2019)=( )
A. 1 B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数且f(-2)=-3,当x≥0时,f(x)=ax-1,其中a>0且a≠1.
(1)求![]() 的值;
的值;
(2)求函数f(x)的解析式;
(3)已知g(x)=log2x,若对任意的x1∈[1,4],存在![]() 使得f(mx1)+1≥g(x2)(其中m≥0)成立,求实数m的取值范围.
使得f(mx1)+1≥g(x2)(其中m≥0)成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com