
已知函数 ,
, ,其中
,其中 的函数图象在点
的函数图象在点 处的切线平行于
处的切线平行于 轴.
轴.
(1)确定 与
与 的关系; (2)若
的关系; (2)若 ,试讨论函数
,试讨论函数 的单调性;
的单调性;
(3)设斜率为 的直线与函数
的直线与函数 的图象交于两点
的图象交于两点 (
( )证明:
)证明: .
.
(1)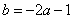 ;(2)当
;(2)当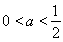 时,函数
时,函数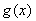 在
在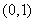 单调递增,在
单调递增,在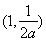 单调递减;在
单调递减;在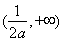 上单调递增;当
上单调递增;当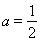 时,函数
时,函数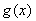 在
在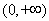 上单调递增;当
上单调递增;当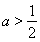 时,函数
时,函数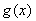 在
在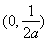 上单调递增,在
上单调递增,在 单调递减;在
单调递减;在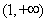 上单调递增.(3)详见解析。
上单调递增.(3)详见解析。
【解析】
试题分析:(1)由导数的几何意义可知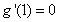 ,即可得
,即可得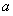 与
与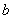 的关系。(2)先求导数,及其零点,判断导数符号,即可得原函数增减变化,注意分类讨论。(3)由
的关系。(2)先求导数,及其零点,判断导数符号,即可得原函数增减变化,注意分类讨论。(3)由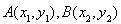 可得
可得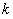 。然后分别证明不等式的左右两侧,两侧不等式的证明均需构造函数,再利用函数的单调性证明。
。然后分别证明不等式的左右两侧,两侧不等式的证明均需构造函数,再利用函数的单调性证明。
试题解析:【解析】
(1)依题意得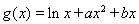 ,则
,则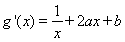
由函数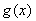 的图象在点
的图象在点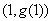 处的切线平行于
处的切线平行于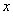 轴得:
轴得: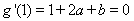
 ∴
∴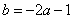 4分
4分
(2)由(1)得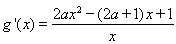
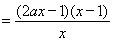
∵函数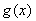 的定义域为
的定义域为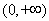
①当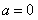 时,
时,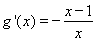
由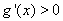 得
得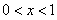 ,由
,由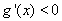 得
得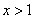 ,
,
即函数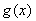 在(0,1)上单调递增,在
在(0,1)上单调递增,在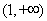 单调递减;
单调递减;
②当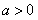 时,令
时,令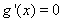 得
得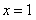 或
或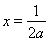 ,
,
若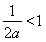 ,即
,即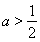 时,由
时,由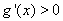 得
得 或
或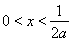 ,由
,由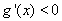 得
得 ,
,
即函数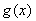 在
在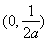 ,
,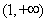 上单调递增,在
上单调递增,在 单调递减;
单调递减;
若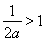 ,即
,即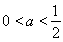 时,由
时,由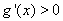 得
得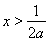 或
或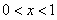 ,由
,由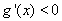 得
得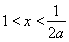 ,即函数
,即函数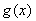 在
在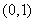 ,
,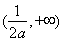 上单调递增,在
上单调递增,在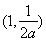 单调递减;
单调递减;
若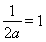 ,即
,即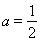 时,在
时,在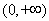 上恒有
上恒有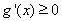 ,即函数
,即函数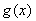 在
在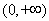 上单调递增.
上单调递增.
综上得:当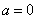 时,函数
时,函数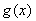 在(0,1)上单调递增,在
在(0,1)上单调递增,在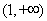 单调递减;
单调递减;
当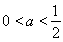 时,函数
时,函数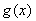 在
在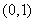 单调递增,在
单调递增,在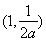 单调递减;在
单调递减;在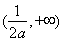 上单调递增;
上单调递增;
当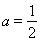 时,函数
时,函数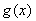 在
在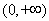 上单调递增,
上单调递增,
当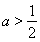 时,函数
时,函数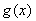 在
在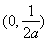 上单调递增,在
上单调递增,在 单调递减;在
单调递减;在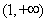 上单调递增.
上单调递增.
9分
(3)依题意得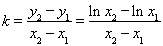 ,证
,证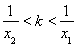 ,即证
,即证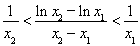

因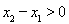 ,即证
,即证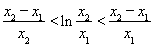 . 令
. 令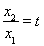 (
(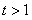 ),即证
),即证 (
(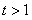 )
)
令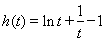 (
(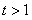 ),则
),则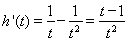
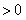
∴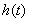 在(1,+
在(1,+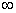 )上单调递增,
)上单调递增,
∴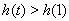 =0,即
=0,即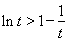 (
(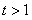 )①
)①
再令m(t)=lnt t+1, =
=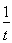 1<0, m(t)在(1,+∞)递减,
1<0, m(t)在(1,+∞)递减,
∴m(t)<m(1)=0,即lnt<t 1 ②
综合①②得 (
(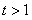 ),即
),即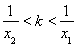 . 14分
. 14分
考点:1导数及导数的几何意义;2用导数分析函数的单调性;3用单调性证明不等式。


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:选择题
已知随机变量X~B(6,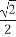 ),则P(-2≤X≤5.5)=( )
),则P(-2≤X≤5.5)=( )
(A) (B)
(B) (C)
(C) (D)
(D)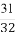
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:填空题
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.设ξ为取出的4个球中红球的个数,则P(ξ=2)= .
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数 ,
, 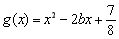 .
.
(Ⅰ)当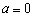 时,求曲线
时,求曲线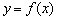 在点
在点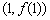 处的切线方程;
处的切线方程;
(Ⅱ)当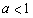 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅲ)当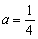 时,函数
时,函数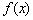 在
在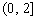 上的最大值为
上的最大值为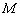 ,若存在
,若存在 ,使得
,使得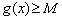 成立,求实数b的取值范围.
成立,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年陕西省咸阳市高考模拟考试(一)理科数学试卷(解析版) 题型:选择题
某产品在某零售摊位上的零售价x(元)与每天的销售量y(个)统计如下表:据上表可得回归直线方程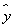 =b
=b +a中的b=-4,据此模型预计零售价定为15元时,销售量为 ( )
+a中的b=-4,据此模型预计零售价定为15元时,销售量为 ( )

A.48 B.49 C.50 D.51
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷2练习卷(解析版) 题型:填空题
已知a,b,c分别为△ABC的三个内角A,B,C的对边,若a2=b2+c2-bc, =
= +
+ ,则tan B的值等于________.
,则tan B的值等于________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com