
分析 (1)利用三角函数恒等变换的应用化简函数解析式可得f(x)=2cos(x+$\frac{π}{3}$)+1,利用周期公式可求函数f(x)的最小正周期,利用余弦函数的图象和性质可求f(x)的值域.
(2)由α∈(-π,0),且f(α-$\frac{π}{6}$)=$\frac{13}{5}$,可求cos(α+$\frac{π}{6}$)=$\frac{4}{5}$,解得sin(α+$\frac{π}{6}$)=±$\frac{3}{5}$,讨论可求sin2(α+$\frac{π}{6}$),cos2(α+$\frac{π}{6}$)的值,由sin(2α+$\frac{π}{12}$)=sin[2(α+$\frac{π}{6}$)-$\frac{π}{4}$]即可计算求值.
解答 解:(1)∵f(x)=2cos2$\frac{x}{2}$-$\sqrt{3}$sinx=1+cosx-$\sqrt{3}$sinx=2cos(x+$\frac{π}{3}$)+1,
∴函数f(x)的最小正周期为2π.
∵cos(x+$\frac{π}{3}$)∈[-1,1],
∴f(x)=2cos(x+$\frac{π}{3}$)+1∈[-1,3].
(2)∵α∈(-π,0),且f(α-$\frac{π}{6}$)=2cos(α-$\frac{π}{6}$+$\frac{π}{3}$)+1=$\frac{13}{5}$,
∴解得:α+$\frac{π}{6}$∈(-$\frac{5π}{6}$,$\frac{π}{6}$),cos(α+$\frac{π}{6}$)=$\frac{4}{5}$,
∴sin(α+$\frac{π}{6}$)=±$\frac{3}{5}$,
①当sin(α+$\frac{π}{6}$)=$\frac{3}{5}$时,
∴sin2(α+$\frac{π}{6}$)=2sin(α+$\frac{π}{6}$)cos(α+$\frac{π}{6}$)=$\frac{24}{25}$,
cos2(α+$\frac{π}{6}$)=cos2(α+$\frac{π}{6}$)-sin2(α+$\frac{π}{6}$)=$\frac{7}{25}$,
∴sin(2α+$\frac{π}{12}$)=sin[2(α+$\frac{π}{6}$)-$\frac{π}{4}$]=$\frac{\sqrt{2}}{2}$sin2(α+$\frac{π}{6}$)-$\frac{\sqrt{2}}{2}$cos2(α+$\frac{π}{6}$)=$\frac{\sqrt{2}}{2}$×$\frac{24}{25}$-$\frac{\sqrt{2}}{2}$×$\frac{7}{25}$=$\frac{17\sqrt{2}}{50}$.
②当sin(α+$\frac{π}{6}$)=-$\frac{3}{5}$时,
∴sin2(α+$\frac{π}{6}$)=2sin(α+$\frac{π}{6}$)cos(α+$\frac{π}{6}$)=-$\frac{24}{25}$,
cos2(α+$\frac{π}{6}$)=cos2(α+$\frac{π}{6}$)-sin2(α+$\frac{π}{6}$)=$\frac{7}{25}$,
∴sin(2α+$\frac{π}{12}$)=sin[2(α+$\frac{π}{6}$)-$\frac{π}{4}$]=$\frac{\sqrt{2}}{2}$sin2(α+$\frac{π}{6}$)-$\frac{\sqrt{2}}{2}$cos2(α+$\frac{π}{6}$)=$\frac{\sqrt{2}}{2}$×(-$\frac{24}{25}$)-$\frac{\sqrt{2}}{2}$×$\frac{7}{25}$=-$\frac{31\sqrt{2}}{50}$.
点评 本题主要考查了三角函数恒等变换的应用,周期公式,余弦函数的图象和性质,考查了计算能力和分类讨论思想,考查了转化思想,属于基本知识的考查.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{6}$ | B. | $\frac{16\sqrt{3}}{3}$ | C. | $\frac{16}{3}$ | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
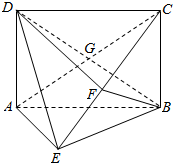 如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC和BD交于点G.
如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC和BD交于点G.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{b^2}{a}$ | B. | $\frac{b^2}{c}$ | C. | $\frac{c^2}{a}$ | D. | $\frac{c^2}{b}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com