
【题目】已知直线 ![]() :
: 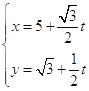 (t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为
(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为 ![]() .
.
(1)将曲线C的极坐标方程化为直坐标方程;
(2)设点M的直角坐标为 ![]() ,直线l与曲线C的交点为A,B,求|MA||MB|的值.
,直线l与曲线C的交点为A,B,求|MA||MB|的值.
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中, ![]() 为正三角形,平面
为正三角形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 的体积;
的体积;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请确定点
?若存在,请确定点![]() 的位置并证明;若不存在,说明理由.
的位置并证明;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=﹣3x2+a(6﹣a)x+b,a,b为实数.
(1)当b=﹣6时,解关于a的不等式f(1)>0;
(2)若不等式f(x)>0的解集为(﹣1,3),求实数a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各项均为正数的数列{an}中,a1=1,Sn是数列{an}的前n项和,对任意n∈N* , 有2Sn=2pan2+pan﹣p(p∈R)
(1)求常数p的值;
(2)求数列{an}的通项公式;
(3)记bn= ![]() ,求数列{bn}的前n项和T.
,求数列{bn}的前n项和T.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系 ![]() 中,以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系.已知曲线
中,以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系.已知曲线 ![]() (t为参数),曲线
(t为参数),曲线 ![]() ;
;
(1)将曲线 ![]() 化成普通方程,将曲线
化成普通方程,将曲线 ![]() 化成参数方程;
化成参数方程;
(2)判断曲线 ![]() 和曲线
和曲线 ![]() 的位置关系.
的位置关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com