
【题目】△ABC的内角A、B、C的对边分别为a、b、c,已知![]() .
.
(1)求角C;(2)若c=2![]() ,求△ABC的面积S的最大值.
,求△ABC的面积S的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)已知等式利用正弦定理化简,整理后根据sinA不为0求出cosC的值,进而确定出sinC的值;
(2)由cosC,c的值,利用余弦定理列出关系式,再利用基本不等式求出ab的最大值,即可确定出S的最大值.
试题解析:
(1)∵2a=![]() csinA﹣acosC,
csinA﹣acosC,
∴由正弦定理可得:2sinA=![]() sinCsinA﹣sinAcosC,
sinCsinA﹣sinAcosC,
∵sinA≠0,
∴可得:2=![]() sinC﹣cosC,解得:sin(C﹣
sinC﹣cosC,解得:sin(C﹣![]() )=1,
)=1,
∵C∈(0,π),可得:C﹣![]() ∈(﹣
∈(﹣![]() ,
,![]() ),
),
∴C﹣![]() =
=![]() ,可得:C=
,可得:C=![]() .
.
(2)∵由(1)可得:cosC=﹣![]() ,
,
∴由余弦定理,基本不等式可得:12=b2+a2+ab≥3ab,即:ab≤4,(当且仅当b=a时取等号)
∴S△ABC=![]() absinC=
absinC=![]() ab≤
ab≤![]() ,可得△ABC面积的最大值为
,可得△ABC面积的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】随着我市九龙江南岸江滨路建设的持续推进,未来市民将新增又一休闲好去处,据悉南江滨路建设工程规划配套建造一个长方形公园ABCD,如图所示,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成,已知休闲区A1B1C1D1的面积为4000m2 , 人行道的宽度分别为4m和10m.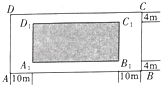
(1)若休闲区的长A1B1=x m,求公园ABCD所占面积S关于x的函数S(x)的解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线 ![]() (t为参数),
(t为参数), ![]() (
( ![]() 为参数).
为参数).
(1)化 ![]() ,
, ![]() 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)过曲线 ![]() 的左顶点且倾斜角为
的左顶点且倾斜角为 ![]() 的直线
的直线 ![]() 交曲线
交曲线 ![]() 于
于 ![]() 两点,求
两点,求 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线 ![]() :
: 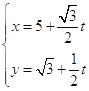 (t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为
(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的坐标方程为 ![]() .
.
(1)将曲线C的极坐标方程化为直坐标方程;
(2)设点M的直角坐标为 ![]() ,直线l与曲线C的交点为A,B,求|MA||MB|的值.
,直线l与曲线C的交点为A,B,求|MA||MB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答
(1)设全集为R,A={x|3<x<7},B={x|4<x<10},求R(A∪B)及(RA)∩B.
(2)C={x|a﹣4≤x≤a+4},且A∩C=A,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点
的左焦点![]() 的离心率为
的离心率为![]() 是
是![]() 和
和![]() 的等比中项.
的等比中项.
(1)求曲线![]() 的方程;
的方程;
(2)倾斜角为![]() 的直线过原点
的直线过原点![]() 且与
且与![]() 交于
交于![]() 两点,倾斜角为
两点,倾斜角为![]() 的直线过
的直线过![]() 且与
且与![]() 交于
交于![]() 两点,若
两点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,且离心率为
,且离心率为![]() ,点
,点![]() 为椭圆上一动点,
为椭圆上一动点, ![]() 内切圆面积的最大值为
内切圆面积的最大值为![]() .
.
(1)求椭圆的方程;
(2)设椭圆的左顶点为![]() ,过右焦点
,过右焦点![]() 的直线
的直线![]() 与椭圆相交于
与椭圆相交于![]() 两点,连接
两点,连接![]() 并延长分别交直线
并延长分别交直线![]() 于
于![]() 两点,以
两点,以![]() 为直径的圆是否恒过定点?若是,请求出定点坐标;若不是,请说明理由.
为直径的圆是否恒过定点?若是,请求出定点坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知10件不同产品中共有4件次品,现对它们进行一一测试,直至找到所有次品为止.
(1)若恰在第5次测试,才测试到第一件次品,第10次才找到最后一件次品的不同测试方法数有多少种?
(2)若恰在第5次测试后,就找出了所有次品,则这样的不同测试方法数有多少种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com