
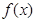 是定义在
是定义在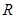 上以
上以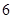 为周期的函数,
为周期的函数,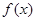 在
在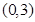 内单调递减,且
内单调递减,且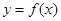 的图象关于直线
的图象关于直线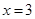 对称,则下面正确的结论是( )
对称,则下面正确的结论是( )A.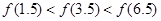 | B.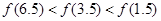 |
C.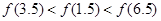 | D.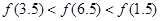 |


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源:不详 题型:解答题

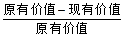 ×100%;在切割过程中的重量损耗忽略不计)
×100%;在切割过程中的重量损耗忽略不计)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 可以以每份0.1元的价格退回报社。在一个月(以30天计算)里,有20天每天可卖出400份,其余10天每天只能卖出250份,但每天
可以以每份0.1元的价格退回报社。在一个月(以30天计算)里,有20天每天可卖出400份,其余10天每天只能卖出250份,但每天 从报社买进的份数必须相同,这个推主每天从报社买进多少份,才能使每月所获的利润最
从报社买进的份数必须相同,这个推主每天从报社买进多少份,才能使每月所获的利润最 大?并计算他一个月最多可赚得多少
大?并计算他一个月最多可赚得多少 元?
元?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com