
 x.……(3分)
x.……(3分)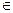 [1,9],从而满足条件(2).(5分)
[1,9],从而满足条件(2).(5分) x,即4lg x-3≤
x,即4lg x-3≤ x对于x
x对于x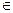 [10,1000]恒成立. ……(6分)
[10,1000]恒成立. ……(6分) x(10≤x≤1000),则g′(x)=
x(10≤x≤1000),则g′(x)=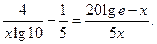 …(8分)
…(8分)
 ∴g′(x) <0对于x
∴g′(x) <0对于x 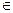 [10,1000]恒成立.
[10,1000]恒成立. ×10=-1<0,
×10=-1<0, x≤0,即4lg x-3≤
x≤0,即4lg x-3≤ x对于x
x对于x 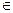 [10,1000]恒成立.从而满足条件(3).
[10,1000]恒成立.从而满足条件(3). 符合奖励方案的要求. …………………(12分)
符合奖励方案的要求. …………………(12分)

 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源:不详 题型:解答题
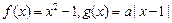 .
.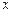 的方程
的方程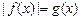 只有一个实数解,求实数
只有一个实数解,求实数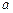 的取值范围;
的取值范围;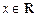 时,不等式
时,不等式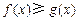 恒成立,求实数
恒成立,求实数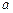 的取值范围;
的取值范围;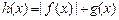 在区间
在区间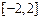 上的最大值(直接写出结果,不需给出演算步骤).
上的最大值(直接写出结果,不需给出演算步骤).查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 在定义域内是增函数;③函数
在定义域内是增函数;③函数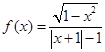 图象关于原点对称;④既是奇函数又是偶函数的函数一定是
图象关于原点对称;④既是奇函数又是偶函数的函数一定是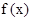 ="0"
="0" 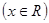 ; ⑤函数y=f(x+2)图象与函数y=f(2-x)图象关于直线x=2对称;其中正确命题的个数为:( )
; ⑤函数y=f(x+2)图象与函数y=f(2-x)图象关于直线x=2对称;其中正确命题的个数为:( )| A.0个 | B.1个 | C.2个 | D.3个 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 时间x(月份) | 1 | 2 | 3 | … | 11 | 12 |
| 销售数量y1(万件) | 1.7 | 1.8 | 1.9 | … | 2.7 | 2.8 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
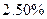 保持不变,到2015年9月1日将所有的存款和利息全部取出,他可取回的钱数约为
保持不变,到2015年9月1日将所有的存款和利息全部取出,他可取回的钱数约为  【 】
【 】| A.11314元 | B.53877元 | C.11597元 | D.63877元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com