
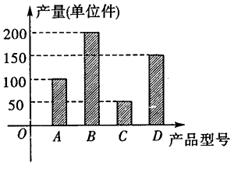
 (3)从A、C型号的产品中随机的抽取3件,用
(3)从A、C型号的产品中随机的抽取3件,用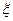 表示抽取A种型号的产品件数,求
表示抽取A种型号的产品件数,求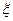 的分布列和数学期望。
的分布列和数学期望。 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
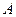 、科目
、科目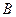 依次进行,只有当科目
依次进行,只有当科目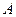 成绩合格时,才可以继续参加科目
成绩合格时,才可以继续参加科目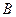 的考试。每个科目只允许有一次补考机会,两个科目成绩均合格方可获得该项合格证书,现在某同学将要参加这项考试,已知他每次考科目
的考试。每个科目只允许有一次补考机会,两个科目成绩均合格方可获得该项合格证书,现在某同学将要参加这项考试,已知他每次考科目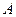 成绩合格的概率均为
成绩合格的概率均为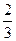 ,每次考科目
,每次考科目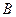 成绩合格的概率均为
成绩合格的概率均为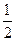 。假设他在这项考试中不放弃所有的考试机会,且每次的考试成绩互不影响,记他参加考试
。假设他在这项考试中不放弃所有的考试机会,且每次的考试成绩互不影响,记他参加考试 的次数为
的次数为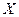 。
。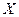 的分布列和均值;
的分布列和均值;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
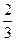 ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为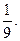
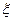 ,求
,求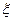 的分布列与均值E
的分布列与均值E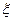 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
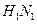 病毒暴发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如下表:
病毒暴发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个流感样本分成三组,测试结果如下表:| | A组 | B组 | C组 |
| 疫苗有效 | 673 |  | 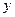 |
| 疫苗无效 | 77 | 90 |  |
 的值;
的值;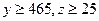 ,求不能通过测试的概率.
,求不能通过测试的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.99.9℅ | B.99℅ 患胃病 未患胃病 合计 生活无规律 5 15 20 生活有规律 40 10 50 合计 45 25 70 |
| C.没有充分的证据显示有关 | D.1℅ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com