
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,且经过点
,且经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 与
与![]() 轴正半轴的交点,
轴正半轴的交点,![]() 上是否存在两点
上是否存在两点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形?若存在,请说明满足条件的
为直角顶点的等腰直角三角形?若存在,请说明满足条件的![]() 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.
【答案】(1)![]() (2)存在,3个
(2)存在,3个
【解析】
(1)根据题意列出方程组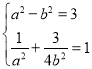 ,解方程组即可.
,解方程组即可.
(2)首先设![]() 所在直线的方程为
所在直线的方程为![]() ,直线
,直线![]() 所在的方程为
所在的方程为![]() .联立直线方程和椭圆方程,解方程求得
.联立直线方程和椭圆方程,解方程求得![]() 的坐标,同理求出
的坐标,同理求出![]() 的坐标.根据
的坐标.根据![]() ,解方程即可求出
,解方程即可求出![]() 的值,再讨论
的值,再讨论![]() 的值,即可判断符合三角形的个数.
的值,即可判断符合三角形的个数.
(1)由题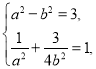 ,解得
,解得![]() ,
,![]() .
.
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)存在,理由如下:
由题意可知,直角边![]() 不可能垂直或平行于
不可能垂直或平行于![]() 轴,
轴,
故可设![]() 所在直线的方程为
所在直线的方程为![]() ,
,
不妨设![]() ,则直线
,则直线![]() 所在的方程为
所在的方程为![]() .
.
联立方程![]() 消去
消去![]() ,并整理得
,并整理得![]() ,
,
解得![]() ,
,
将![]() 代入
代入![]() 可得
可得![]() ,
,
所以点![]() 的坐标为
的坐标为![]() .
.
所以![]() .
.
同理可得![]() ,
,
由![]() ,得
,得![]() ,
,
所以![]() ,则
,则![]() ,
,
解得![]() 或
或![]() .
.
当![]() 斜率
斜率![]() 时,
时,![]() 斜率
斜率![]() ;
;
当![]() 斜率
斜率![]() 时,
时,![]() 斜率
斜率![]() ;
;
当![]() 斜率
斜率![]() 时,
时,![]() 斜率
斜率![]() .
.
综上所述,符合条件的三角形有3个.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,直线
,直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标和
的坐标和![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的指数,空气质量按照AQI大小分为六级,0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;大于300为严重污染.某环保人士从当地某年的AQI记录数据中,随机抽取了15天的AQI数据,用如图所示的茎叶图记录.根据该统计数据,估计此地该年空气质量为优或良的天数约为__________.(该年为366天)
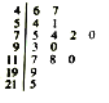
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个工厂在某年连续10个月每月产品的总成本y(万元)与该月产量x(万件)之间有如下一组数据:
x | 1.08 | 1.12 | 1.19 | 1.28 | 1.36 | 1.48 | 1.59 | 1.68 | 1.80 | 1.87 |
y | 2.25 | 2.37 | 2.40 | 2.55 | 2.64 | 2.75 | 2.92 | 3.03 | 3.14 | 3.26 |
(1)通过画散点图,发现可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)①建立月总成本y与月产量x之间的回归方程;
②通过建立的y关于x的回归方程,估计某月产量为1.98万件时,此时产品的总成本为多少万元?
(均精确到0.001)
附注:①参考数据:![]() ,
,
![]() ,
,
②参考公式:相关系数 ,
,
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生会开展了一次关于“垃圾分类”问卷调查的实践活动,组织部分学生干部在几个大型小区随机抽取了共50名居民进行问卷调查.调查结束后,学生会对问卷结果进行了统计,并将其中一个问题“是否知道垃圾分类方法(知道或不知道)”的调查结果统计如下表:
年龄(岁) |
|
|
|
|
|
|
频数 |
|
| 14 | 12 | 8 | 6 |
知道的人数 | 3 | 4 | 8 | 7 | 3 | 2 |
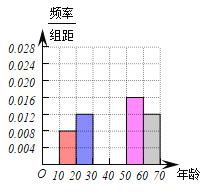
(1)求上表中的![]() 的值,并补全右图所示的的频率直方图;
的值,并补全右图所示的的频率直方图;
(2)在被调查的居民中,若从年龄在![]() 的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率.
的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】武汉市摄影协会准备在2020年1月举办主题为“我们都是追梦人”摄影图片展,通过平常人的镜头记录国强民富的幸福生活,摄影协会收到了来自社会各界的大量作品,打算从众多照片中选取100张照片展出,其参赛者年龄集中![]() 在之间,根据统计结果,做出频率分布直方图如图:
在之间,根据统计结果,做出频率分布直方图如图:

(1)求频率直方图中![]() 的值,并根据频率直方图,求这100位摄影者年龄的中位数;
的值,并根据频率直方图,求这100位摄影者年龄的中位数;
(2)为了展示不同年龄作者眼中的幸福生活,摄影协会按照分层抽样的方法,计划从这100件照片中抽出20个最佳作品,并邀请相应作者参加“讲述照片背后的故事”座谈会.
①在答题卡上的统计表中填出每组相应抽取的人数:
年龄 |
|
|
|
|
|
人数 |
②若从年龄在![]() 的作者中选出2人把这些图片和故事整理成册,求这2人中至少有1人的年龄在
的作者中选出2人把这些图片和故事整理成册,求这2人中至少有1人的年龄在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】苹果是人们日常生活中常见的营养型水果.某地水果批发市场销售来自5个不同产地的富士苹果,各产地的包装规格相同,它们的批发价格(元/箱)和市场份额如下:
产地 |
|
|
|
|
|
批发价格 |
|
|
|
|
|
市场份额 |
|
|
|
|
|
市场份额亦称“市场占有率”.指某一产品的销售量在市场同类产品中所占比重.
(1)从该地批发市场销售的富士苹果中随机抽取一箱,求该箱苹果价格低于![]() 元的概率;
元的概率;
(2)按市场份额进行分层抽样,随机抽取![]() 箱富士苹果进行检验,
箱富士苹果进行检验,
①从产地![]() 共抽取
共抽取![]() 箱,求
箱,求![]() 的值;
的值;
②从这![]() 箱苹果中随机抽取两箱进行等级检验,求两箱产地不同的概率;
箱苹果中随机抽取两箱进行等级检验,求两箱产地不同的概率;
(3)由于受种植规模和苹果品质的影响,预计明年产地![]() 的市场份额将增加
的市场份额将增加![]() ,产地
,产地![]() 的市场份额将减少
的市场份额将减少![]() ,其它产地的市场份额不变,苹果销售价格也不变(不考虑其它因素).设今年苹果的平均批发价为每箱
,其它产地的市场份额不变,苹果销售价格也不变(不考虑其它因素).设今年苹果的平均批发价为每箱![]() 元,明年苹果的平均批发价为每箱
元,明年苹果的平均批发价为每箱![]() 元,比较
元,比较![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com