
分析 (I)利用作差比较,结合已知条件即可证得结论;
(Ⅱ)展开多项式,结合基本不等式以及已知条件即可证得结论.
解答 证明:(Ⅰ)∵|1-ab|2-|a-b|2=1+a2b2-a2-b2=(a2-1)(b2-1).
∵|a|>1,|b|>1,∴a2-1>0,b2-1>0.
∴|1-ab|2-|a-b|2>0,故有|1-ab|>|a-b|;
(Ⅱ)(am+bn)(bm+an)=abm2+(a2+b2)mn+abn2
=(a2+b2)mn+ab(m2+n2)≥(a2+b2)mn+2abmn=mn(a2+2ab+b2)=mn(a+b)2,
∵a+b=1,
∴(am+bn)(bm+an)≥mn(a+b)2=mn.
∴(am+bn)(bm+an)≥mn.
点评 本题考查了不等式的证明,考查了基本不等式的应用,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
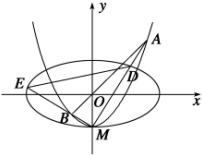 如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,x轴被曲线C2:y=x2-b截得的线段长等于C1的长半轴长.C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A,B,两直线MA,MB分别与C1相交于点D,E.
如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,x轴被曲线C2:y=x2-b截得的线段长等于C1的长半轴长.C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A,B,两直线MA,MB分别与C1相交于点D,E.| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com