
分析 联解方程组,得直线与抛物线交于点A(-3,-6)和B(1,2),因此求出函数3-x2-2x在区间[-3,1]上的定积分值,就等于所求阴影部分的面积,接下来利用积分计算公式和法则进行运算,即可得到本题的答案.
解答 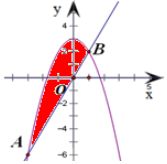 解:由y=2x与y=3-x2,解得x=-3或1,
解:由y=2x与y=3-x2,解得x=-3或1,
∴直线y=2x与抛物线y=3-x2交于点A(-3,-6)和B(1,2),
∴两图象围成的阴影部分的面积为:
S=${∫}_{-3}^{1}$[(3-x2)-2x]dx=(3x-$\frac{1}{3}$x3-x2)${|}_{-3}^{1}$=(3×1-$\frac{1}{3}$×13-12)-[3×(-3)-$\frac{1}{3}$×(-3)3-(-3)2]=$\frac{32}{3}$,
故答案为:$\frac{32}{3}$.
点评 本题求直线与抛物线围成的阴影部分图形的面积,着重考查了定积分计算公式和定积分的几何意义等知识,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |b-a|≥1 | B. | 2a<2b | C. | lg$\frac{a}{b}$<0 | D. | 0<$\frac{b}{a}$<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com